Dalga Denkleminin Çözümü
The source free wave equation:
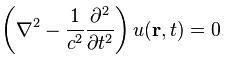
\(u(\vec{r},t)\): The scalar wave function. It satisfies this eq. in free space. \(c\): wave speed. For EM waves, the speed of light. Dalga fonk.u, konum ve zamanın fonksiyonu. Seperation of variables yapılabilir.
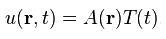
Denkleme koyduğunda elde edilen form:
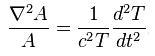
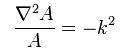 | | 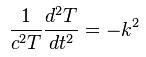 |
| Birinci denklemi yeniden düzenlersek Helmholtz denklemini elde ederiz: |
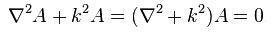 |
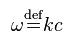 | 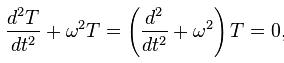 |
The solutions of paraxial Helmholtz equation are the Hermite-Gaussian and Laguerre-Gaussian modes.
What is paraxial approximation? Paraxial Helmholtz denkleminin, sadece Helmholtz denkleminden farkı?
Wave equation \(\nabla^2\tilde{E}-\frac{n^2}{c^2}\frac{\partial^2\tilde{E}}{\partial t^2}=0\) has two important solutions:
- Plane wave
\(\tilde{E}=E_0 e^{i(kz-\omega t+\phi)}\): propagation in \(+z\) direction
- Spherical wave
\(\tilde{E}=\frac{A}{r}e^{i(kr-\omega t+\phi)}\)
- In plane wave, we have \(E_0\). It is constant. We cannot create this with a physically realizable beam.
- When the constant, \(E_0\), is replaced by \(U(x,y,z)\), it means a departure from a "pure" plane wave.
It can describe a physically realizable beam.
\(U(x,y,z)\) provides
Let's put \(\tilde{E}=U(x,y,z) e^{i(kz-\omega t+\phi)}\) into wave equation.
Let's assume that we align the beam and its angular spread becomes sufficiently small. It varies very slowly with \(z\).
So \(|\frac{\partial^2 U}{\partial z^2}|\ll 2k |i\frac{\partial U}{\partial z}|\).
Then, \(U(x,y,z)\) satisfies paraxial equation \(\frac{\partial^2 U}{\partial x^2}+\frac{\partial^2 U}{\partial y^2}+2ik\frac{\partial U}{\partial z}=0.\) This eq. is also deemed as scalar wave eq.
To conclude, in plane wave solution, first case is the no variation in field as it propagates in \(z\) direction case. As a second case, when we create very small variation in field as it propagates in \(z\), we obtain e.g. laser beam. Paraxial approximation is the second case.
Gaussian Beams - Enrique Galvez
A solution is introduced to paraxial wave equation:
\(U_0(x,y,z)=A g(x,z) h(y,z) e^{ik(x^2+y^2)/[2q(z)]}e^{ip(z)}\)
Substitution of this solution into paraxial wave equation gives solution for \(g\) and \(h\) in terms of Hermite polynomials. Final solution:
\(U_{n,m}(x,y,x)=A\frac{1}{\omega (z)} H_n(\frac{\sqrt{2}x}{\omega (z)}) H_m(\frac{\sqrt{2}y}{\omega (z)}) e^{-(x^2+y^2)/\omega (z)^2} e^{ik(x^2+y^2)/[2R(z)]} e^{-i\varphi (z)}\)
Guoy phase: \(\varphi (z)=(n+m+1)\tan^{-1}{(\frac{z}{z_R})}\)
Amplitude: \(A=\sqrt{\frac{2^{1-n-m}}{\pi n! m!}}\)
\(U_{1,0}(x,y,z)=\frac{1}{\sqrt{\pi}}\frac{1}{\omega (z)}H_1(\frac{\sqrt{2}x}{\omega (z)}) H_0(\frac{\sqrt{2}y}{\omega (z)}) e^{-\frac{x^2}{\omega (z)^2}} e^{\frac{ikx^2}{2R(z)}} e^{-i\varphi (z)}\)
\(U_{1,0}(x,y,z)=\frac{1}{\sqrt{\pi}}\frac{1}{\omega (z)} (2 (\frac{\sqrt{2}}{\omega (z)}) x) (1) e^{-\frac{x^2}{\omega (z)^2}} e^{\frac{ikx^2}{2R(z)}} e^{-i\varphi (z)} = HG_{10}\)
\(HG_{10}\) seems 1D (to have x dependency) in transverse. But intensity profile seems 2D (to have also y dependency). How to solve this contradiction?
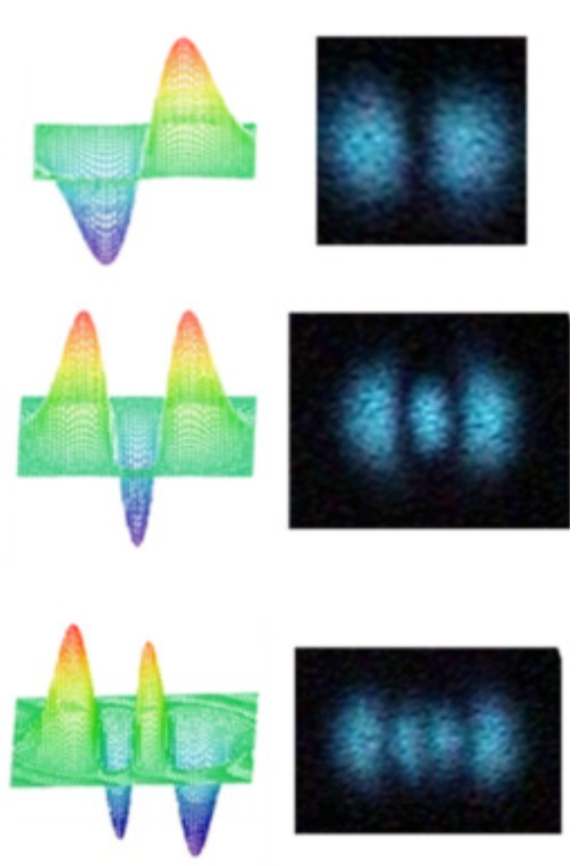
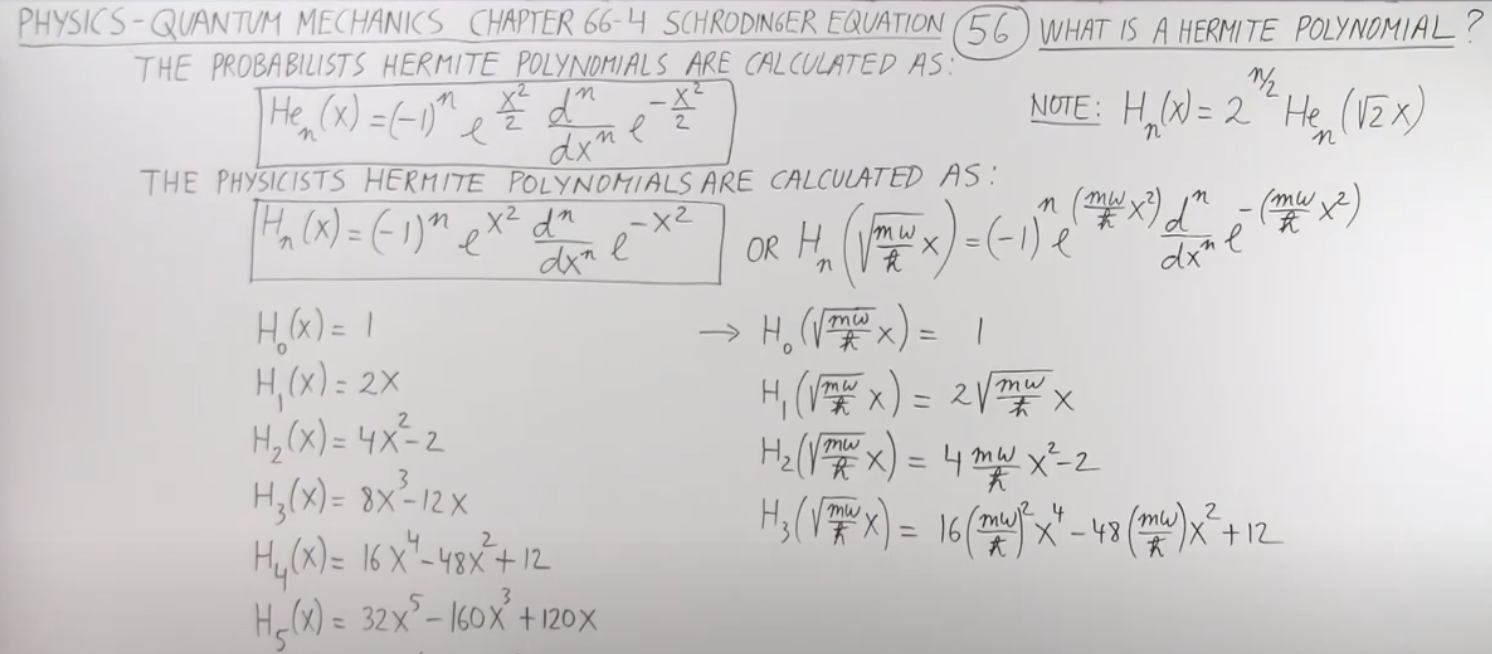
Quantum-like nonseparable structures in optical beams
\(\vec{E}(\vec{\rho},z,t)=2 Re[\vec{U}(\vec{\rho},z) e^{ik(z-ct)}]\)
\(\vec{\rho}=\hat{x}x+\hat{y}y\)
\(\vec{U}(\vec{\rho},z)\): analytic signal. complex amplitude of the field.
Classical entanglement in polarization metrology
The electric field can be written as \(\vec{E}(\vec{r},t) = Re[\vec{E}(\vec{r}) e^{i(kz-wt)}]\) where
\(\vec{E}(\vec{r})=(A_0 \hat{e}_x + A_1 \hat{e}_y)\psi(\vec{r})\)
\(\psi(\vec{r})\): spatial mode of the beam.
\(\vec{r}=x\hat{e}_x+y\hat{e}_y+z\hat{e}_z\): position vector
\(\hat{e}_x, \hat{e}_y, \hat{e}_z\): unit vectors in x, y, z directions
\(A_0, A_1\): complex numbers. the amplitudes of the electric field along the x-and y-axis. (Elektrik alana istediğin polarizasyonu kazandırmak için bu terimlere dikkat edeceksin.)
Dalga Denkleminin Çıkarılışı
Gergin bir ipteki çok küçük bozulmanın denklemi, dalga denklemini veriyor. İp gergin olduğu için diğer yöndeki bozulma söz konusu.
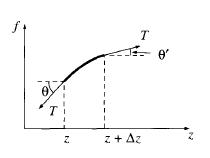
z ile z+delta z arasındaki parça üstündeki net kuvvet (T ip gerilmesi):
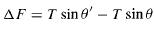
Bu kuvvet enine uygulanmaktadır (transverse force). Enine, boyuna dalgalar diye ayırdığımızda boyuna dalgaların bu noktada değişimle ilgisi var mı şimdilik kalsın.
sin tan ile yerdeğiştirebilir çünkü bozulma çok küçüktür.

İpteki küçük bozulmalar bu denklemi sağlar.