Faz uzayında olasılık yoğunluğu
Faz uzayının bileşenleri konum ve momentum (\(q, p\)). Klasik istatistiksel mekanikte bir sistemin gerçekte hareketi, faz uzayında phase trajectory ile ifade edilir. Kuantum istatistiksel mekanikte bir sistemin konum ve momentumu aynı anda tam olarak (with exact precision) belirlenemez. Bu sebeple "\(\Delta q \Delta p\) hacminde bulunma" olarak düşünelim. Sistemin \(T\) süresinde \(\Delta q\Delta p\) hacminde bulunma sürece miktarı (süresi) \(\Delta t\) olsun. Bu iki değerden olasılık elde edebiliriz.
\(\omega =\lim_{T\to\infty} \frac{\Delta t}{T}\)
\(T\) sürekli artsa bile oran bir değere yakınsar. \(\omega\) olasılıktır (probability).
Sonsuz küçük hacim \(dq dp\). Olasılık ayrıca aşağıdaki gibi yazılmış:
\(d\omega=\varrho (q,p) dqdp\)
\(\varrho (q,p)\), yoğunluktur, olasılık yoğunluğu.
Yoğunluğu tüm \(q\) ve \(p\)'ler üzerinden integre edersen normalisation condition gereği \(1\) bulursun:
\(\int \varrho dp dq=1\)
Aynı birimli oranlar olasılığı hep verir bence. Ben \(\varrho=\frac{1}{\int dqdp}\) derdim. O zaman, zaman cinsinden yoğunluk da \(\frac{1}{T}\) mi? Problemimiz için \(\frac{1}{T}\), \(\frac{1}{\int dqdp}\)'ye eşdeğer mi? Her olasılığın bir yoğunluğu var demek ki.
O zaman kuantumda \(\lvert \braket{i}{\psi}\rvert^2=p(i)\)'de
- \(p(i)\): olasılık
- \(\lvert \braket{i}{\psi}\rvert^2\): yoğunluk
- \(\ket{\psi}=\sum_i c_i\ket{i}\)'deki \(c_i\): genlik.
\(p(q_m, p_m)=Tr\Big(\widehat{\rho} \widehat{\pi} (q_m, p_m)\Big)\)'da
- nihai matrisin diagonal elemanları yoğunluklar
- trace işleminin sonucu, olasılık.
Thermal equilibrium = thermodynamic equi. = statistical equi.
Bir sistemde macroscopic physical quantities, ortalama değerlerini gösteriyorsa (zaman içinde ortalama değerler tekrar ediyorsa) termal dengededir. Termal dengedeki sistemin toplam enerjisi sabittir. 1'den fazla sistemi birleştirirsen enerjileri additive büyüklük olup toplanır. Termal dengedeki ayrı sistemlerin enerjileri sabitken birleştirildiğinde toplanır ve toplam sistemin toplam enerjisi değişir. Sebep: termal dengede olan sistemler kapalı sistemlerdir. Sistem, o sınır koşullarına göre dengeye gelmiştir. Fakat birleştirme yaptığında sınırlar değişir, dolayısıyla dengede sistemler bile tekrar dengeye gelme sürecine girerler.
Klasik istatistikten kuantum istatistiğe geçiş
İstatistiksel bağımsızlık
2 subsystem'in fiziksel özellikleri (karakteristikleri) birbirini etkilemiyorsa bunlar bağımsızdır. Etkileşim yok. 2 alt sistemin bir fiziksel özelliği direk çarpılır.
Mikrodurum
Bir sistemi oluşturan parçacıkların her birinin konum, momentum veya kuantum sayıları verilerek belirlenen farklı durumuna mikrodurum denir.
Bölüşüm fonksiyonu
Toplam durumlar kümesidir. Ama enerjilere ait küme. Z sayısı enerjilere ait ama enerji biriminde değil, birimsiz. Mikrodurum sayısı ve enerjileri ile belirlenir. Ama formülde mikrodurum sayısı yoktur. Makro ölçekte eksponansiyel ile ifade edilir. Enerjinin topluluğa, exponansiyeli oranında katkısı var. Parçacık sayısı cinsinden değil, enerji cinsinden yazıyoruz. Parçacık sıklaşması ile enerji seviyesi sıklaşması aynı değil. Enerji ve parçacık sayısı grafiğini gör.
Bir kapalı sistem alalım. Bunun içinde açık bir alt sistem alalım. Alt sistemin özellikleri "1" indisi ile, geriye kalan kısım "2" indisi (suffix) ile işaretlensin.
- Toplam sistemin mikrodurum sayısı, iki alt sistemin mikrodurum sayılarının çarpımıdır. (Demek ki etkileşmiyorlar, bağımsızlar.)
- E1 + E2 = E = sabit
- E2 = E - E1 kullanalım.
Denge durumunda dahi sistemi oluşturan moleküller/atomlar hareket halindedir. Elemanlar çarpışarak anlık ısı alış verişi yapar, hızlarını, konumlarını değiştirirler. Isı alış verişi interaction değil midir? Biz ise az önce bağımsızlık özelliğinden yola çıkarak mikrodurumları direk çarparak toplam mikrodurum sayısını bulduk. Isı alış verişiyle alt sistemlerin enerjileri (E1 ve E2) değişir. 2 nolu sisteme göre küçük olduğu için sadece E1 mi değişir yoksa E2 de değişir mi? Yani E-E1 çok küçük bir değer olup sabit mi kabul ederiz E2'yi? E ve E1 arasında çok fark mı olur? Bence mikrodurum sayısı ile mikroduruma ait enerjiye aynı muamele yapılmalı? Tatmin olmuş değilim ama verilen yanıt: Enerji değişimi mikro ölçekte, Toplam mikrodurum sayısı ya da 1 nolu alt sistemin mikrodurum sayısı makro ölçekte, bundan dolayı 2 alt sistemi istatistiksel bağımsızmış gibi mikrodurumlarını çarpabiliyoruz. Sistem makroölçekte
istatistiksel bağımsız, mikro ölçekte değil gibi. Ama sistem değişkenleri/parametreleri sabittir. T, V, N sistem değişkenleridir; E1 anlık olarak değişebildiği ve T, V, N'yi değiştirmediği için sistem değişkeni değildir. Denge durumunda toplam sistem için tek değişen E1 (iç enerji)dir.
Denge durumunda dahi çarpışmalar var dedik. "Thermal equilibrium presupposes mechanical equilibrium." Denge durumundaki body'ler için birbirleri üzerine etkiyen basınç sabittir.
- Büyük ölçekte (sistemin tamamında) mekanik denge var, termal denge var, toplam enerji sabit.
- Sistemin elemanlarına inersek çarpışmalar var, anlık enerji alışverişi var; termal denge yok çünkü mekanik denge yok.
Mikroduruma geçme sebebimiz
Sistemin (örneğin gazın) makrodurumu aynı kaldığı halde mikrodurumları sürekli değişir. Aynı makroduruma karşılık gelen mikrodurumlar önem arz ediyormuş.
Isı (dQ): Sistem durum değiştirirken alınıp verilen enerji türüdür ısı.
Heat capacity = Specific heat: Heat capacity, thermal response function'dır.
Isı değişimi için PV=nRT formülüne hangi aşamayla geçtik?
Heat capacity (özgül ısı), sistemin birim sıcaklık değişiminde sisteme verilmesi gereken veya sistemden alınması gereken birim ısıdır.
- Sbt hacimde: dQ=ncvdT
- Sbt basınçta: dQ=ncpdT
Klasik makinelerde alınan ısı (dQ) tamamıyla iş üretiminde (dW) kullanılmaz, sistemin iç enerjisindeki artışla (dE) kayıp meydana gelir: dQ=dW+dE. Sistemin kinetik + potansiyel enerjilerindeki artış, sistemin iş üretmesi anlamına gelir (sistem çevre üzerine iş yapıyor). dW teriminin içinde kinetik + potansiyel enerji değişimi var. dQ=PdV+dE. Sisteme parçacık sayısı ekleme/çıkarmaya izin verirsek dQ=PdV+dE+mdN (mü: kimyasal potansiyel). Tersinir süreçler için dQ=SdT yazılabilir. SdT=PdV+dE+mdN olur.
İç enerji (internal energy) (bazen E bazen U): Bir sistemin mekanik (kinetik + potansiyel) enerjilerini sistemin enerjisinden (veya sisteme verilen enerjiden) çıkardığında elde ettiğin enerji türü. İç enerji durum fonksiyonudur. Buradaki KE+PE makroskopik KE+PE'dir.
İç enerji, sistemin mikroskopik bileşenleriyle (atomlar ve moleküller ile) ilgili enerjidir. İç enerji deyince şunları kapsar:
- moleküllerin random translational, rotational, vibrational kinetik enerjileri;
- moleküllerin içindeki random vibrational potansiyel enerji (yani molekülün içindeki atomlar arasında olan kuvvetler ile ilgili);
- moleküller arasındaki elektriksel potansiyel enerji (etkileşim enerjisi).
Başka bir iç enerji tanımı: Tüm mikrodurumların enerjilerinin ortalamasıdır. Bunun için her bir Ei değerini kendi olasılığıyla çarpıp toplarız:
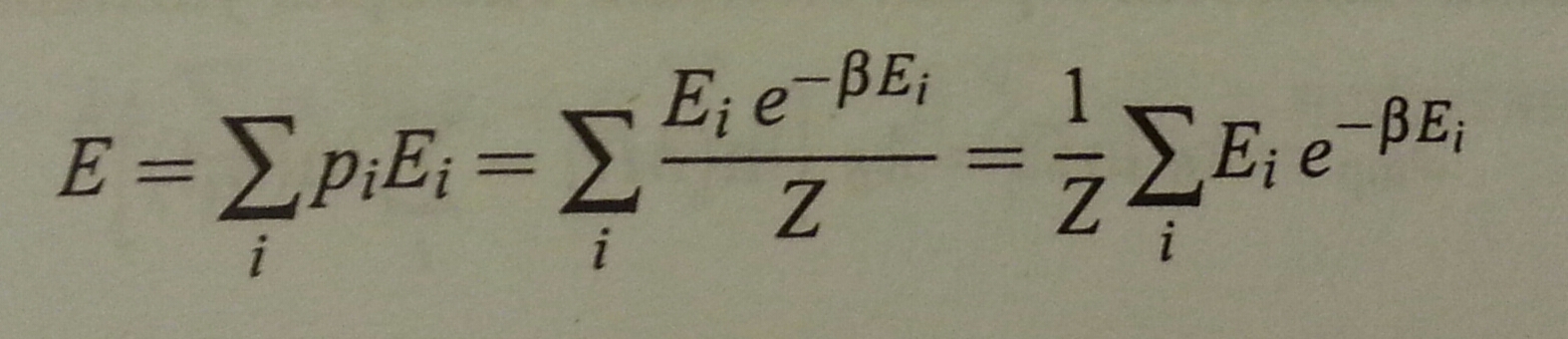
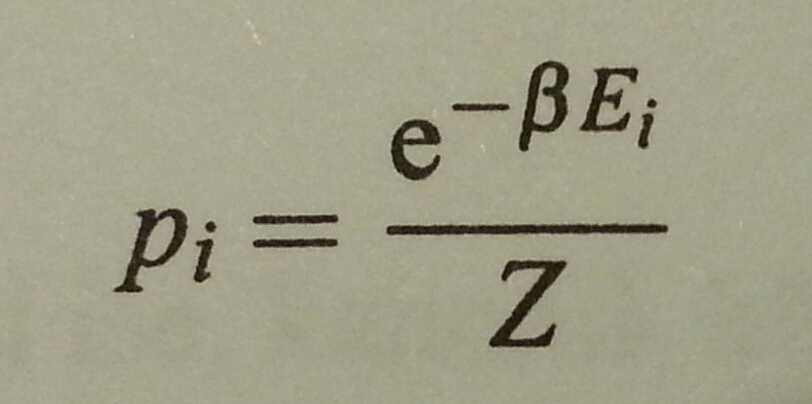
E
i enerjili durumun olasılığı bölüşüm fonk cinsinden.
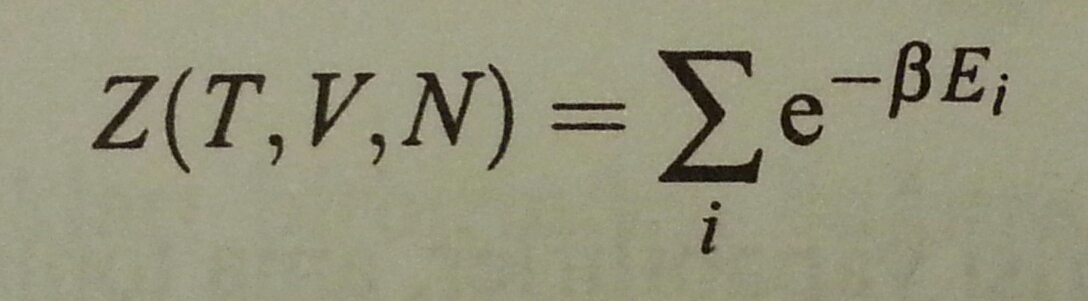
Bölüşüm fonk
Netice olarak iç enerji, sistemin klasik ölçekte hissettirdiği etkileri sistemden çıkardığımızda elimizde kalan kuantum ölçekteki etkilerdir.
İç enerji, giren - çıkan'dır.
Tam diferansiyel büyüklükler yoldan bağımsızdır ve durum değişkeni olur. Tersinmez süreçlerde tam diferansiyel uygulayamayız çünkü tam diferansiyel çevrim içerir ama tersinmez irreversible'dır, geri dönüşü yok, süreci (termodinamik değişkenleri) tersine işletemezsin.
Bir sistemin initial ve final state'lerine göre iç enerjisi E belirlenebilir. E, tam diferansiyeldir. Ancak enerji değişimi dE'ye karşılık gelen sistemin aldığı/verdiği ısı ve yapılan iş unique olarak belirlenemez. Bir sistem cyclic process yaptığında enerji değişimi dE sıfırdır ancak dQ ve dW sıfır olmayabilir, birbirlerini karşılayacak miktarlarda değişmiş olabilirler. Dolayısıyla dE tam diferansiyeldir, dQ veya dW tam diferansiyel değildir.
Sistemin iç enerjisi E, hamilton fonksiyonuymuş. H=KE+PE yazıyoruz. Buradaki KE ve PE, mikroskopik (sistemin iş üretmeyen) tarafına ait olsa gerek. Sisteme enerji verdiğinde, sistemin iç enerjsisi artar. Ama iç enerji, çıktı yaratana kadar artar. Sistemin iç enerjisini daha fazla arttırma kapasitesi kalmayınca çıktı yaratmaya başlar.
Work function: Atomdan bir elektron koparmak için gerekli enerji miktarı. Atoma foton verirsin verirsin, bir noktadan sonra eşik değerini aşar ve bir elektronu serbest bırakır. Metalden elektron atımı için gerekli minimum enerji miktarıdır. Bir fotonun enerjisi hv kadardır (v frekansına bağlı olarak değişir). Bu foton metalik yüzeye çarptığında enerjisini metalik yüzeye aktarır. hv enerjisi bir elektron salınımı için yeterli olmayabilir, yeterli enerji miktarına ulaştığında elektron salınır. Bu enerji miktarına work function denir. Sistemin çıktı yaratması için gerekli enerji miktarıdır. Bu yönüyle iç enerji'ye benzer. İç enerji de iç değişimi ifade eder. Aşağıdaki denklem, sisteme verilen enerji work function ve elektronun kaçma kinetik enerjisinde kullanılır. Ama eşik değerine ulaşmadığın sürece sisteme verdiğin enerji sadece work function üretir.
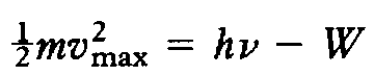
İşi, hacmin değişmesiyle yazıyoruz: dW=PdV. Ama basıncın değişmesi de iş oluyor, yalnız farklı çeşit iş: Hacmin değişmesi "mekanik iş", basıncın değişmesi "ısısal iş"e giriyor.
dx yerdeğiştirmesi dışında her şey sbt:
dW=F*dx
P=F/A
dW=P*A*dx Sistemin A alanının dx kadar ilerlemesi hacmi verir.
dW=P*dV İş, hacmin değişimine bağlı.
Kuvvet değişken:
dP=dF/A
dW=dP*A*x
dW=dP*V
Hacmin sabit tutulup basıncın değişmesi sisteme ısı verilmesi ya da sistemden ısı alınmasıyla olur (sistemin parçacık sayısı değişmiyor kabul edelim). Basıncın değiştirilmesi ısısal (termal) enerji değişimidir. Isı enerjisine ısısal iş diyebiliriz çünkü tanım gereği "W=-delta U" dur. Hacim değişimi, mekanik enerji iken basınç değişimi ısısal enerjidir. Tüm enerji değişimleri iş olarak da adlandırılabilir.
dE/dt=dR/dt + dQ/dt
dR/dt=-P*dV/dt
Nötr parçacıklardan oluşan bir sistemin termal denge noktası ile örneğin negatif yüklü parçacıklardan oluşan bir sistemin termal noktası farklıdır. Nötr sistem homojen dağılım gösterirken yüklü sistemde parçacıklar birbirlerine en uzak noktalara yerleşeceklerdir.
Birbirine karışabilen, farklı karakteristiklere sahip iki sistemin termal denge noktası aynıdır fakat bu noktaya varış süreleri farklı olabilir.
Entropi: Maxwell's demon, termodinamiğin 2.yasası olan "kapalı sistemlerde entropi azalmaz"ı ihlal ediyor.
Senaryo (1.bölüm): kapalı sistemi 2 bölüme (partition) ayıralım, ortada 2 bölüm arasında geçişi sağlayan küçük bir kapı var. Kapı, hızlı molekülleri sağ tarafta yavaş molekülleri sol tarafta toplayacak şekilde kontrol ediliyor. Ve yavaş moleküller solda, hızlılar sağda biriktiğinde sistemin toplam entropisi azalmış oluyor.
Soru: Kapalı sistemin ortasına bir duvar koyduğunda dış koşullarını değiştirmiş oluyorsun, dolayısıyla 2 ayrı kapalı sistem oluşuyor. Enerji, artık toplam enerji kadar değil, entropi, toplanabilir (additive) bir büyüklük olarak artık baştaki entropi kadar değil. Dolayısıyla entropi azaldı! Entropiyi azaltarak işe başladık! 2 ayrı kapalı sistemin toplamı baştaki tek kapalı sisteme denk değildir bence. Bence bir sistemi bölmelere ayırmakla ayırmamak arasında fark var.
Çıkarım: Entropiyi belirleyen, moleküllerin çarpışma miktarı değil, hızları! Doğru mu?
Kapalı sistem başlangıçta dengede olmasın, zamanla dengeye gelsin. Kapalı bir sistemin dengeye gelmesi, sıcaklık, basınç, entropi bakımından homojenize olması demek bence. Yani sistemin her yerinde sıcaklık, basınç, entropi aynı. Yani termodinamik büyüklükler konum ve zamansal olarak ortalama değerleri gösteriyor. Ancak başka örneklerde faz bakımından homojen olmama var. Su-buz veya su-buhar olarak sistemde 2 ayrı faz bulunup denge durumu olabilir. (Bu arada basınçlar eşit olmasaydı basıncı düşük olan tarafa sürekli akış olurdu. Ayrıca 2 fazın kimyasal potansiyelleri (mü1 ve mü2) eşittir. mü1=mü2'nin çıkarımı Fazların Dengesi konusunda yapılıyor.)
Senaryo (2.bölüm): Demon bir hafızaya sahip. Hızları bilmesi için ölçmesi gerekiyor. Hafızası ölçüm sonuçlarıyla dolacak ve hafızada yer açmak için silmeye başlayacak. Bilgi silmek de entropiyi arttırır. Dolayısıyla sistem aslında gaz sistemi ve demon'dan oluşuyor.
Soru: Demon'ın hafızasını çok büyük yaparsın ve ölçüm sonuçlarını uzun süre silmeden muhafaza edersin. Ve entropinin azaldığı durumu gözlersin.
Adyabatik süreç
- Thermally isolated bir sistem alalım. External conditions yeterince yavaş değişiyorsa "adiabatic process"ten geçiyoruz demektir. Sistem enerjisi E=E(q,p,t)'nin fonksiyonudur.
- Adyabatik süreçte sistem, ortalama karakteristiklerini tekrar eder (bir büyüklüğün aldığı değer, ortalama değere saibtlenmiştir). Sistem yaklaşık olarak istatistiksel denge durumundadır.
- Adyabatik süreçte entropi sabittir.
Adyabatik süreçte entropinin dış koşula bağlı olarak yavaş değiştiğini varsayalım:
Eğer external conditions zamana bağlı bir parametre (l) ile tanımlanıyorsa sistem enerjisi E=E(q,p,l) ile tanımlanır. Entropinin zamanla değişimi l'nin zamanla değişimine bağlıdır. dl/dt küçükse dS/dt, dl/dt'nin kuvvetleri cinsinden seriye açılabilir:
- dS/dt=c (dl/dt)0+b (dl/dt)1+a (dl/dt)2+...
- ilk terim kuvveti sıfır olduğu için sıfırdır, sabittir.
- ikinci terim: (+) eğim zamanla artan l, (-) eğim zamanla azalan l yani geriye gidiş, yani tersinir süreç olacaktır. Entropideki yansıması zamanla azalan entropi olacaktır. Ki fiziksel olan, entropinin artmasıdır. Bu terim fiziksel mana taşımaz. (dl/dt)1 'in sonucu negatif olabileceği ve fiziksel durumu tarif etmeyeceği için eledik.
- Fiziksel anlam taşıyan ilk terim, üçüncü terimdir ve entropi-dış koşul ilişkisi bununla ifade edilir: dS/dt=a (dl/dt)2 veya dS/dl=a dl/dt
- l'nin zamanla değişimi sıfıra gittiğinde S'nin değişimi de sıfıra gider. Yani external condition'ın yavaş değiştiği durumda (yani adyabatik süreçte) entropi sabit değerde seyreder.
Shannon entropy
Elimizde n uzunluğunda veri olsun. Her veriyi kodlamak için alfabedeki karakter sayısı (s) kadar seçeneğimiz var: sn. Bundaki bilgi miktarı H(sn)=log(sn) log s tabanında olmalı?!
Bilgi miktarı=bit sayısı. H0(A)=log2A. A=2n
Entropiyle microstate arasındaki ilişki gibi log var.S=kBln(# of microstates) veya # of microstates=eS
Molecule
Molekül, atomların etkileşimdeki denge konumları olan bir konfigürasyondur. Her atom kendi denge konumu etrafında küçük osilasyonlar yapar. Denge noktaları etkileşime ait minimum potansiyel enerji noktalarıdır. Potansiyel enerji:
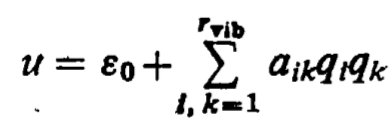
- İlk terim, denge konumundaki potansiyel enerjidir. İkince terim, atomların denge konumundan sapma ile ilgili.
- Potansiyel enerjiye katkı, vibrational hareketten geliyor.
- Vibrasyonel hareket: Örneğin 2 atomlu lineer molekülün atomları birbirine yay ile bağlıymış ve yayın doğrultusu boyunca ikisi de git gel hareketi yapıyorlar.
- n atomlu bir molekülün serbestlik derecesi 3n'dir.
- Momentuma katkı 3n sayıda hareketten gelir.
Foton Gazı
Foton gazı, ısısal denge yapması için bir maddeye ihtiyacı vardır. Foton gazının dengede olabilmesi için bir maddeye ihtiyacı vardır. Vakum ortamında etkileşime girmeden ilerler durur. Gerekli madde katı cisim olmak zorunda değil, ideal gaz da olabilir. Ortamda bir miktar madde olmalı ki foton gazı o maddeyle ısısal dengeyi gerçekleştirsin.
Kapalı bir sistem olsun, içeriye foton gazı ve katı cisim koyalım, hava olmasın. Isısal denge durumunda madde ile fotonların enerjisi aynı mı oluyor? Ya da ısı kapasiteleri ile ilgili. Isısal denge direk ısılarının aynı olması demek olmayabilir. Fotonun Cp'si, maddenin Cp'si işin içine girmiyor mu? Fotonların olduğu bir ortamda bulunan metal ile ahşabın sıcaklıkları farklı? Sıcaklıkların farklı olması ısı kapasiteleriyle alakalı. O zaman ısıları eşit olmamalı? Bu arada ısı kapasitesi kütleyle orantılıymış, fotonun kütlesi sıfırsa ısı kapasitesi sıfır olmalı? O zaman nasıl, ısı sahibi?
Cisim fotonları absorb eder, emit eder, absorb eder, emit eder. Emit etmezse ısınır.
Ya da: foton absorb ediliyor, maddenin molekülleri içindeki elektronlar uyarılıyor, sonra geri emit ediliyor. Foton şiddeti yüksek olduğunda nonlineer etki olup madde ısınıyor. Yine ısısal denge var.