Electric potential energy, electric potential
\(\vec{E}\) çizgileri \(+\)'dan \(-\)'ye.
Sol tarafta \(+\) yükler dizili, sağ tarafta \(-\) yükler.
\(\vec{E}\) soldan sağa yönelmiş.
Ortama serbest noktasal yük koyarsak: The free point charge and electric field are our system.
- Elektrik alan yüke kuvvet uygular. \(\vec{F}=q\vec{E}\)
- Yük serbest olduğu için hareket eder. \(d\vec{s}\)
- Elektrik alan iş yapmış olur. \(W=\vec{F}\cdot d\vec{s}\)
- Work is done by an internal element of the system, not by an external force out of the system. Since total energy is conserved, \(W_{int}+\Delta U=0\).
If an external force does work on the system, the total energy of the system changes, \(W_{ext}=\Delta U\).
\(U\): Potential energy of the charge-field system.
\(\Delta U=U_f-U_i\)
Ayrıca potansiyel enerjinin 0 olduğu bir yer tanımlanır sistemde, \(U=0\). Yükün bu noktaya göre potansiyeli \(U\) olur.
- If we take out charge from the system (\(\frac{U}{q}\)), we obtain a physical quantity depends only on the source charge distribution, \(\frac{U}{q}=V\), \(\frac{\Delta U}{q}=\Delta V\).
\(V\): Potential
\(\Delta V=V_f-V_i\)
\(\Delta V\): Potential difference
Potansiyel \(\Delta V=-\int_i^f \vec{E}\cdot d\vec{s}\) olarak da tanımlanır.
- Charge is \(+\):
\(\vec{F}=+q\vec{E}\)
\(W=qEx\)
\(\Delta U=-qEx\)
- Charge is \(-\):
\(\vec{F}=-q\vec{E}\)
\(W=-qEx\)
\(\Delta U=qEx\)
Bound charges
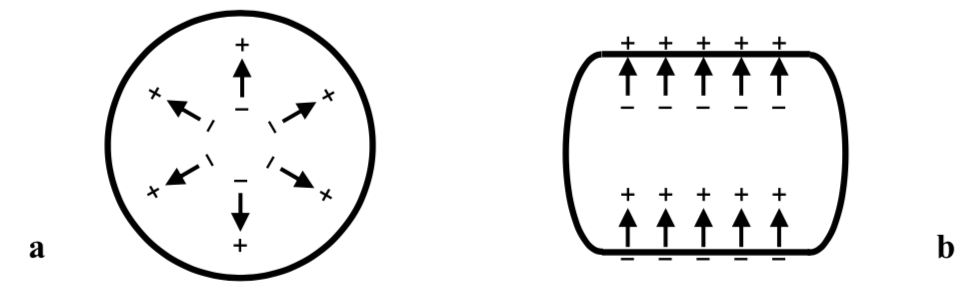
\(P\): Polarization vector. The arrows show the polarization.
- a: P is non-uniform.
\(\vec{\nabla}\cdot\vec{P}\neq 0\)
\(P\)'nin gradient'ı 0 değil, dolayısıyla hacimsel bağlı yük yoğunluğu (volume bound charge density) (\(\rho_b\)) var.
\(-\vec{\nabla}\cdot\vec{P}=\rho_b\)
- b: P is uniform \(\equiv\) no divergence \(\Rightarrow\) \(\rho_b=0\). There is only surface bound charge density (\(\sigma_b\)).
\(\vec{P}\cdot\hat{n}=\sigma_b\)
The bound charges are caused by the polarization.
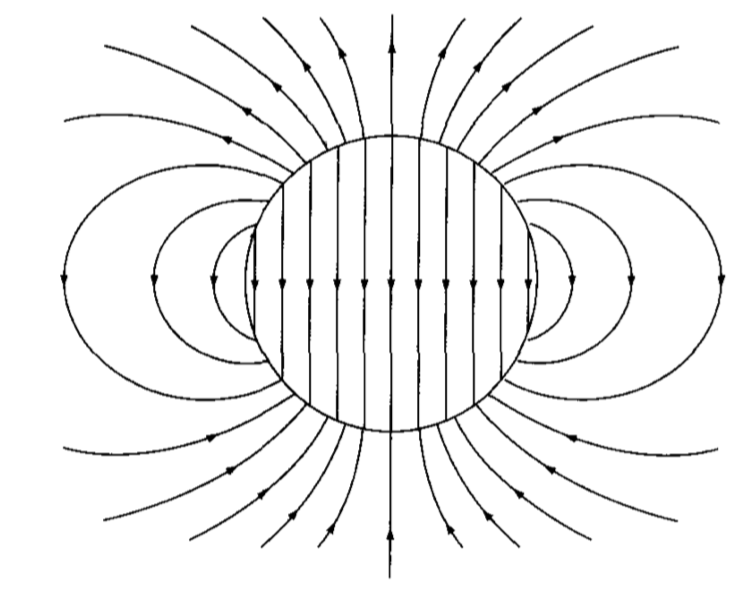
Uniformly polarized sphere. The arrows show the electric field.
Ampere-Maxwell law
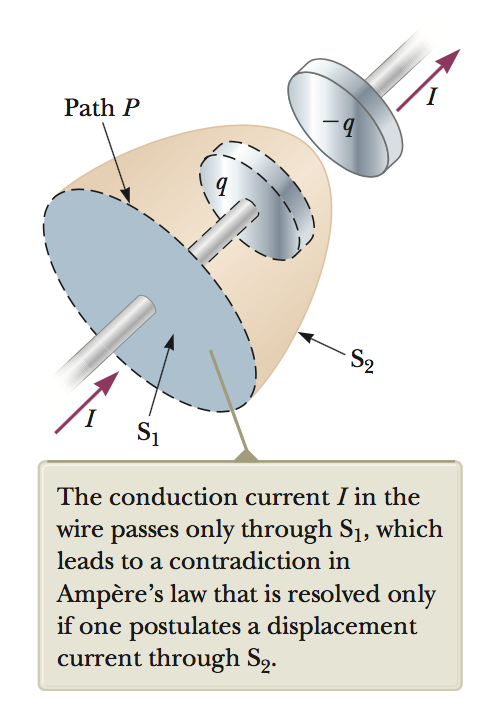
\(\oint \vec{B} \cdot d\vec{s}=\mu_0 I+\mu_0 I_d=\mu_0I+\mu_0\epsilon_0\frac{d\Phi_E}{dt} \)
Akımın tanımı yük hareketi değil! Akım, yük hareketi üzerinden tanımlanmıyor, zaman üzerinden tanımlanıyor., yükün zamanla değişimi üzerinden tanımlanıyor:
\(I\equiv\frac{dQ}{dt}\)
Manyetik alanın oluşumunu yük hareketi üzerinden tanımlama, akım üzerinden tanımla. Önceden akımı yük hareketi üzerinden tanımlayıp, yük hareketi yoksa manyetik alan da yok diyordun. Artık biliyorsun akımın tanımı, zaman üzerinden; manyetik alanın tanımı, akım üzerinden yapılıyor. Dolayısıyla parallel plate capacitor'ün iki tarafında bağlı kabloda akım var. Kapasitör dolana kadar kabloda akım ve parallel conductor'larda yük değişimi var. Kapasitör dolduktan sonra kabloda akım yok, paralel plakalarda da yük değişimi yok. Demek ki akım varken kabloda da (wire) plakalar arasında da manyetik alan var. Dolayısıyla Ampere-Maxwell denkleminin söylediği "kablo etrafında da kapasitör içinde de manyetik alan hesabı yapma" sağlanıyor. Önceden kapasitör sebepli, kapasitör içinde manyetik alan hesaplamak için sebebin yoktu, şimdi var.