Deutsch-Jozsa Algorithm (to be zero or not)
The problem to which this algorithm suggests solution is that there is an input set of all possible values of n bits, there is a function whose global property is to be constant or balanced which means it takes either all the inputs to a constant value or half of the inputs to a value and other half of the inputs to another value. \(f: \{0,1\}^n\rightarrow \{0,1\}\). Element number of input set is \(2^n\). Element number of output set is either 1 or 2. And global propert of \(f\) will be determined. A classical computer solves this problem with \(\frac{2^n}{2}+1\) number of queries. What about a quantum computer uses D-J Alg.? It solves this problem in which number of queries?
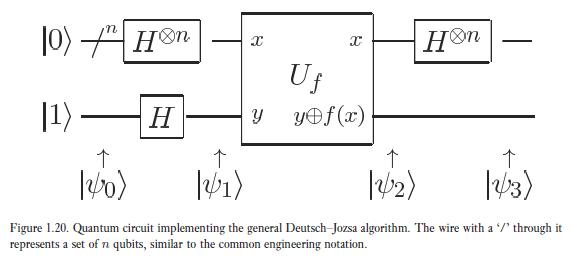
Input state's space is \(2^{n+1}\) dimensional.
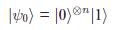
After \(\ket{\psi_0}\), we apply Hadamard gate to \(n+1\) qubits. We combine \(n\) qubits with Kronecker product. Now we have the superposition of all the basis of \(2^n\) dimensional space and the last qubit:
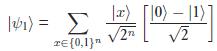
Now, we are in the stage of applying the unitary transformation \(U_f\). n bunch of qubits gidiği gibi çıkıyor, the function \(f(x)\) is applied onto the last qubit only. \(f(x)\) is either constant or balanced, in all the situations the last qubit will change according to \(\ket{0\oplus f(x)}-\ket{1\oplus f(x)}\). Let's say \(f(x)\) is constant and is equal to \(0\). Then, the last qubit remains as it is, n bunch of qubits too. Let's say \(f(x)\) is constant and is equal to \(1\). Then, the last qubit becomes \(\frac{-\ket{0}+\ket{1}}{\sqrt{2}}=-\frac{\ket{0}-\ket{1}}{\sqrt{2}}\). n bunch of qubits expression doesn't change. Only, we see either \(+\) or \(-\) caused by the last qubit. So general expression in case of constant function:
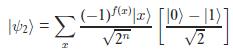
If \(f(x)=0\) for all the inputs, \(\ket{\psi_2}\) has \(+\) sign. If \(f(x)=1\) for all the inputs, \(\ket{\psi_2}\) has \(-\) sign.
\(\ket{\psi_3}=\ket{0}^{\otimes n} (-1)^{f(x)}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
First n-qubit is called as registers, last qubit is called as target qubit. Registers constitute the input set in the problem. Last qubit is just like an ancillary qubit.
Let's assume \(n=2\). If \(f(x)\) is balanced and:
case III:
- \(f(00)=0\)
- \(f(01)=0\)
- \(f(10)=1\)
- \(f(11)=1\)
It means that if 1.qubit is 0, do nothing to 3.qubit. If 1.qubit is 1, flip 3.qubit. (2.kübit etkisiz eleman.)
\(\ket{\psi_1}=\frac{1}{\sqrt{4}}(\ket{00}+\ket{01}+\ket{10}+\ket{11})\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
In \(\ket{\psi_3}\), last qubit will change according to first qubit. So group qubits according to first qubit:
\(\ket{\psi_2}=\frac{1}{\sqrt{4}}\big((\ket{00}+\ket{01})\frac{\ket{0}-\ket{1}}{\sqrt{2}}+(\ket{10}+\ket{11})\frac{\ket{0}-\ket{1}}{\sqrt{2}}\big)\)
If first qubit is 1, flip third qubit:
\(\ket{\psi_2}=\frac{1}{\sqrt{4}}\big((\ket{00}+\ket{01})\frac{\ket{0}-\ket{1}}{\sqrt{2}}+(\ket{10}+\ket{11})\frac{\ket{1}-\ket{0}}{\sqrt{2}}\big)\)
Take \(-\) sign from last qubit and use it in first and second qubit:
\(\ket{\psi_2}=\frac{1}{\sqrt{4}}\big((\ket{00}+\ket{01})\frac{\ket{0}-\ket{1}}{\sqrt{2}}+(-\ket{10}-\ket{11})\frac{\ket{0}-\ket{1}}{\sqrt{2}}\big)\)
\(\ket{\psi_2}=\frac{\ket{0}-\ket{1}}{\sqrt{2}} \frac{\ket{0}+\ket{1}}{\sqrt{2}} \frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
\(\ket{\psi_3}=\ket{10}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
case IV:
- \(f(00)=1\)
- \(f(01)=1\)
- \(f(10)=0\)
- \(f(11)=0\)
It means that if 1.qubit is 0, flip 3.qubit. If 1.qubit is 1, do nothing to 3.qubit.
\(\ket{\psi_3}=-\ket{10}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
case V:
- \(f(00)=0\)
- \(f(01)=1\)
- \(f(10)=0\)
- \(f(11)=1\)
It means that if 2.qubit is 0, do nothing to 3.qubit. If 2.qubit is 1, flip 3.qubit.
\(\ket{\psi_3}=\ket{01}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
case VI:
- \(f(00)=1\)
- \(f(01)=0\)
- \(f(10)=1\)
- \(f(11)=0\)
It means that if 2.qubit is 0, flip 3.qubit. If 2.qubit is 1, do nothing to 3.qubit.
\(\ket{\psi_3}=-\ket{01}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\)
As a result, after the measurement of registers if \(\ket{00}\) is obtained, we understand that \(f(x)\) is a constant function. If other results than \(\ket{00}\) is obtained, we understand that \(f(x)\) is a balanced function. In the generalization, \(\ket{00}\) becomes \(\ket{0}^{\otimes n}\) and while a classical computer solves this problem with \(\frac{2^n}{2}+1\) queries, a quantum computer solves this problem with \(n\) queries.