Quantum Fourier Transform
Ya bir parçacık üstünden düşünelim ya da birden fazla parçacığın oluşturduğu uzayı yeni tek parçacık elemanları üstünden düşünelim. Bu durumda QFT, bir bazı alıp baz setindeki tüm bazların superpozu haline getirir, tüm elemanlar eşit ağırlıkla bulunurlar.
Parçacık tipi qubit ise uzayın boyutu 2n, qutrit'se 3n, ququart'sa 4n'dir. n parçacık sayısı. Eğer 1 parçacık ve bu parçacığa ait N tane boyut varsa uzayın boyutu N1.
QFT circuit for 3 qubits
n qubit varken uzayın 2n=N boyutlu. j=0, 1, 2, ..., N-1. j'ler uzayın bazları.
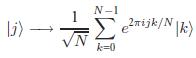
j'nin amacı sbt faz ile çalışabilmek. Farklı j değerleri için farklı sbt faz.
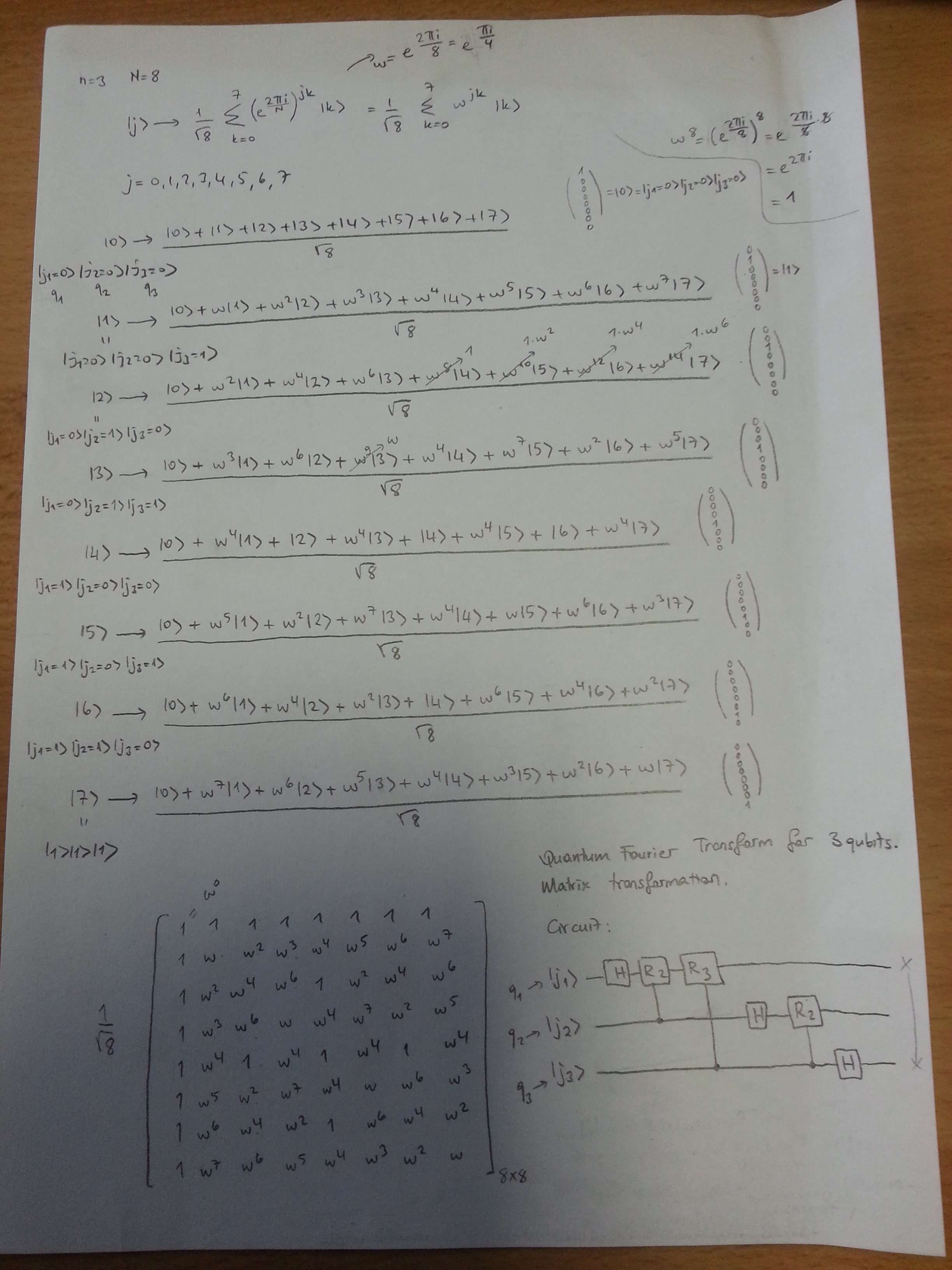
j=0 state'in içinde j1=0, j2=0, j3=0 var. j'ler 3 qubitin değer aldığı durumlar. Devrede etiketlendirdiğin j1, j2, j3 ile buradaki j1, j2, j3 farklı. Dolayısıyla devrede gördüğün j1 üstünden tüm 8 bazın QFT dönüşümünü hesaplayamazsın.
q1, q2, q3 (qubit1, qubit2, qubit3) QFT formülünde açıkça değer almıyor. Bunların oluşturdukları uzay etiketlendiriliyor.
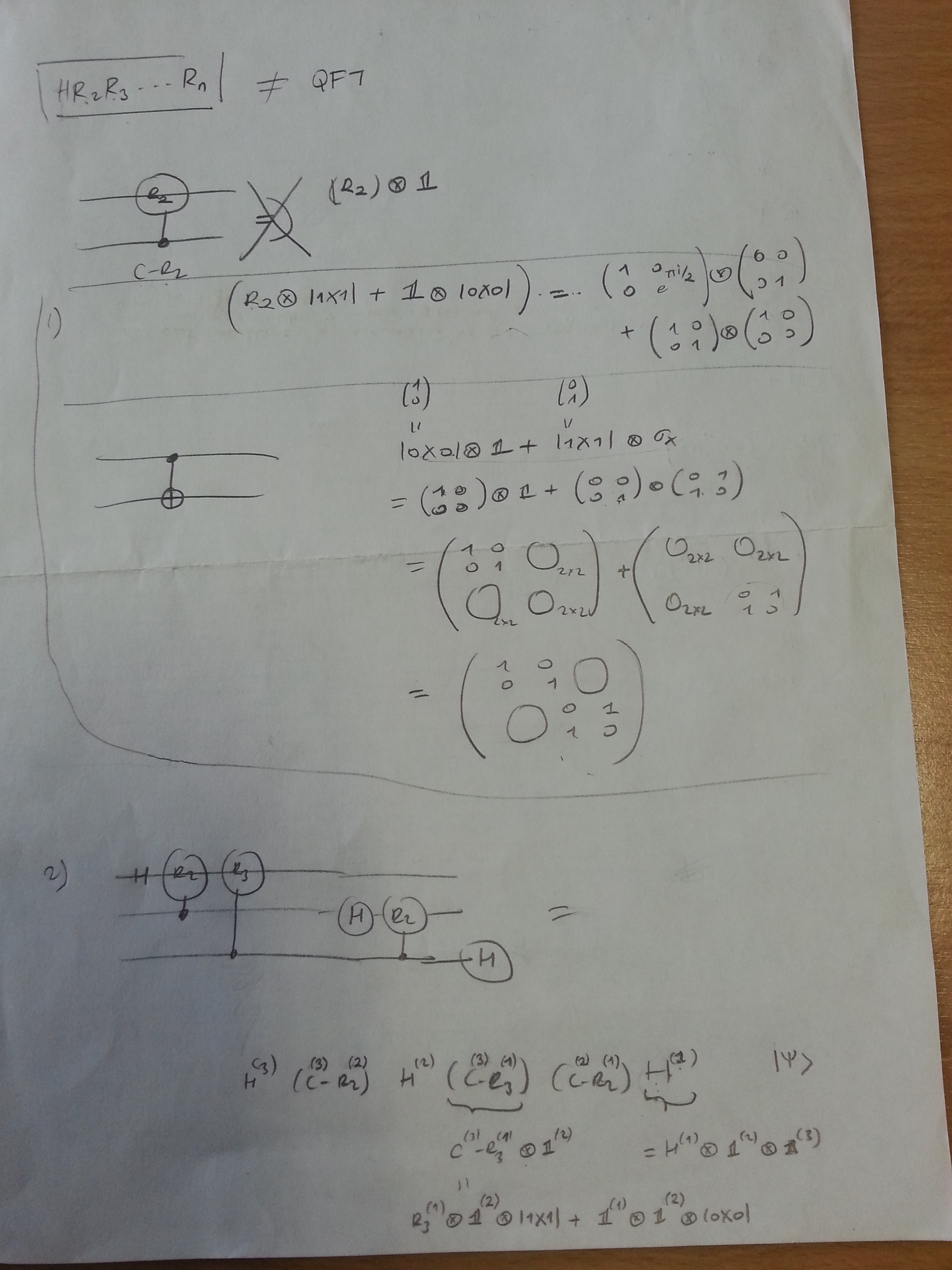
Transformation matrix'ini formül üstünden değil de matrislerin çarpımı üstünden bulmak istersen izlemen gereken yol aşağıdaki gibi olmalı.
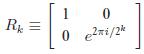
R2, R3 rotation matrix'lerini kontrollü yapıyorsun. Kontrol ya da işlem yapacağı qubit'in indeksi matrisin üstünde yazan sayı.
d-dimensional Hadamard gate:
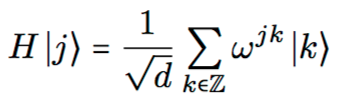
1 qutrit için Hadamard gate:
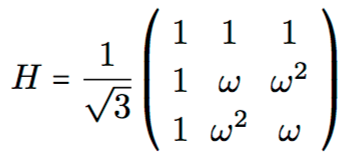
Burada w=e
(2pi i)/3
Görünen o ki yukarıdaki en genel matris ifadesi aynı, sadece parçacığın boyut sayısına göre N değişiyor ve w'nun döngüsü değişiyor.O zaman Hadamard, QFT, rotasyon matrisi farkı?
Aşağıda x'in 1 artma aşamasına gelindiğinde y=0 olması döngüye girdiğini gösterir: e(2pi i) yerine.
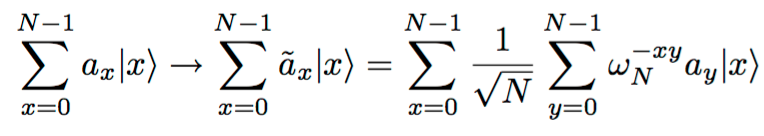
Her bir x böyle değişir:
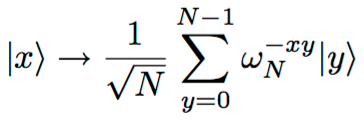
Yukarıda matris gösteriminde ilk sütunun tamamen 1 olması, döngüden.
En üstteki fotoğrafta 8 adet bazın dönüşümlerini yaptın. QFT, esas olarak bir quantum state'in amplitude'larını değiştirir. Yani 8 adet baz ile yazılmış bir state'in katsayılarını değiştirir. Yukarıdaki matristen yola çıkarsan:
from psi=0+1+2+3+4+5+6+7
to psi=
0(1+1+1+1+1+1+1+1) +
1(1+w2+w3+w4+w5+w6+w7) +
2(1+w2+w4+w6+1+w2+w4+w6) +
3(1+w3+w6+w+w4+w7+w2+w5) +
4(1+w4+1+w4+1+w4+1+w4) +
5(1+w5+w2+w7+w4+w+w6+w3) +
6(1+w6+w4+w2+1+w6+w4+w2) +
7(1+w7+w6+w5+w4+w3+w2+w)
2 kübitin oluşturduğu uzayı, 2 parçacık üstünden düşünelim ve QFT formülünü yazalım:
\(\ket{\Psi_{nm}}=\frac{1}{\sqrt{d}}\sum_{j=0}^{d-1}e^{\frac{2 \pi i}{d}jn}\ket{j}\ket{j+m mod d}\) d: bir parçacığın boyutu yani 2. n, m, j=0, 2.
\(\ket{\Psi_{00}}=\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})\\
\ket{\Psi_{01}}=\frac{1}{\sqrt{2}}(\ket{01}+\ket{10})\\
\ket{\Psi_{10}}=\frac{1}{\sqrt{2}}(\ket{00}+e^{\frac{2 \pi i}{2}1.1}\ket{11})=\frac{1}{\sqrt{2}}(\ket{00}-\ket{11})\\
\ket{\Psi_{11}}=\frac{1}{\sqrt{2}}(\ket{01}+e^{\frac{2 \pi i}{2}1.1}\ket{10})=\frac{1}{\sqrt{2}}(\ket{01}-\ket{10})\)
Birden fazla parçacık bazında Bell bazları oldular.
2 kübitin oluşturduğu uzayı tek parçacık üstünden düşünelim:
\(\ket{n}=\frac{1}{\sqrt{d}}\sum_{j=0}^{d-1}e^{\frac{2 \pi i}{d}jn}\ket{j}\). d: uzayın boyutu yani 4. n, j=0, 1, 2, 3
\(\ket{0}=\frac{1}{\sqrt{4}}(\ket{0}+\ket{1}+\ket{2}+\ket{3})\\
\ket{1}=\frac{1}{\sqrt{4}}(\ket{0}+e^{\frac{2 \pi i}{4}1.1}\ket{1}+e^{\frac{2 \pi i}{4}2.1}\ket{2}+e^{\frac{2 \pi i}{4}3.1}\ket{3})=\ket{1}=\frac{1}{2}(\ket{0}+e^{\frac{\pi i}{2}}\ket{1}+e^{\pi i}\ket{2}+e^{\frac{3 \pi i}{2}}\ket{3})=\frac{1}{2}(\ket{0}+i\ket{1}-\ket{2}-i\ket{3})\\
\ket{2}=\frac{1}{\sqrt{4}}(\ket{0}+e^{\frac{2 \pi i}{4}1.2}\ket{1}+e^{\frac{2 \pi i}{4}2.2}\ket{2}+e^{\frac{2 \pi i}{4}3.2}\ket{3})=\frac{1}{2}(\ket{0}+e^{\pi i}\ket{1}+e^{2 \pi i}\ket{2}+e^{3 \pi i}\ket{3})=\frac{1}{2}(\ket{0}-\ket{1}+\ket{2}-\ket{3})\\
\ket{3}=\frac{1}{\sqrt{4}}(\ket{0}+e^{\frac{2 \pi i}{4}1.3}\ket{1}+e^{\frac{2 \pi i}{4}2.3}\ket{2}+e^{\frac{2 \pi i}{4}3.3}\ket{3})=\frac{1}{2}(\ket{0}+e^{\frac{3 \pi i}{2}}\ket{1}+e^{3 \pi i}\ket{2}+e^{\frac{9 \pi i}{2}}\ket{3})=\frac{1}{2}(\ket{0}+-i\ket{1}+\ket{2}+i\ket{3})\)
2 yöntem aynı sonucu vermedi.
Notes
I think QFT can be the change of domain. It is like from time domain to frequency domain. Periyodik gibi görünmeyen bir fonksiyonun periyodik bazda ifade edilmesi demek. Dönüştürüldüğü bazda, periyodik fonksiyonlar farklı ağırlıklarda bulunabilir.
QFT is the transformation of a complex problem to another problem whose solution is known.
QFT: From computational basis to Fourier basis (periodic functions).
QFT is the transformation of quantum mechanical amplitudes of a vector we concern with.
Örneğin periyodik görünmeyen bir fonksiyonu periyodik bir fonksiyona çevirip sonra da "period finding" yapıyorsun.
QFT'nin bir uygulaması quantum phase estimation (QPE). QPE'de phase kick back var. Aradığın objenin fazını ancilla'lardan okuyorsun.
An n-th degree polynomials can be written in terms of a unitary matrix.
Hence the eigenvalues of the matrix will be the roots of the polynomial.
Then, the eigenvalues of the unitary matrix can be found by QPE algorithm.
As a result, an application of QPE is finding the roots of a polynomial.
An eigenvalue is most generally a complex number but for unitary operators it is real.
Real numbers is a subspace of complex numbers. They can be expressed by using phase equals either 0 or \(\pi\).
With this two value how will we obtain the values greater than 1 or decimal numbers? Or something will change in this perspective.
Finally, the eigenvector whose eigenvalue wanted to be determined is subjected to QPE algorithm.
"Quantum Phase Estimation Algorithm for Finding Polynomial Roots"