Quantum Teleportation

Alice ve Bob farklı konumlardadır. Alice, dolaşık kübit çiftinden birine, Bob diğerine sahiptir. Dolanık çift olarak \(\ket{\beta_{00}}\)'ı alsınlar. Bu \(\ket{\beta_{00}}\) değil, 4 Bell state'ten herhangi biri olabilirdi, aşağıdaki örnek için \(\ket{\beta_{00}}\)'ı alalım. A ve B dolanık kübitlerinin ne olduğunu biliyorlar. Alice dolanık kübitini kullanarak bir başka kübitin durumunu telenakledecek. Telenakil yapılacak durum 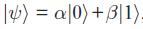olsun. Telenakil yapılacak durumun ne olduğunu Alice ve Bob bilmiyor.

Alice devreye input olarak 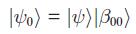'ı giriyor. Devre şu şekilde:

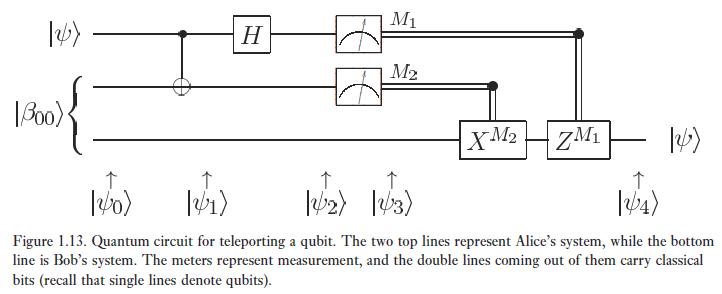
\(\ket{\psi_0}\)'ın açık hali:

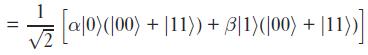
Qubit'ini CNOT gate'e gönderdikten sonra \(\ket{\psi_1}\)'i elde ediyor:

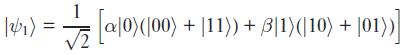
Hadamard gate işlem yaptıktan sonra \(\ket{\psi_2}\)'yi elde ediyor:

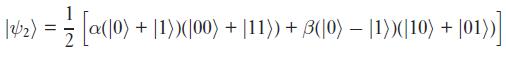
Gruplama yapalım:

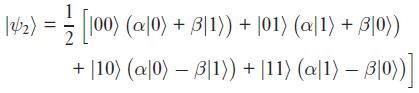
Burada 4 lineer bağımsız computational basis'i görüyoruz. Alice ölçüm yapar ve 00'ı elde ederse Bob'un qubit'i teleport edilecek qubit'in state'ine dönüşmüş demektir. Bunun gibi Alice'in ölçüm sonuçları şu şekildedir. Alice'te sol taraf varsa Bob'da sağ tarafı vardır.

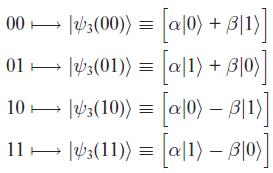
M1, M2 ölçümleriyle Alice'in kendi dolanık qubit'ini ve 2. qubit'i ölçtükten sonra elde ettiği şey, birer 1 veya 0'dır (Psi3). Bunlar artık classical bittir.

Bob'un kendi qubit'inin aldığı state'i bilmesi için Bob'a Alice tarafından ölçüm sonucu söylenmelidir. Bu nokta ışıktan hızlı iletişimin olmadığını gösterir. Bob kendi qubit'inin state'ini öğrendikten sonra psi'sini recover yapıp baştaki halini elde edebilir. Bob 4 Pauli transformation'dan (sigma x, sigma y, sigma z, birim matris) birini uygulayarak kendi qubit'ini döndürecek:



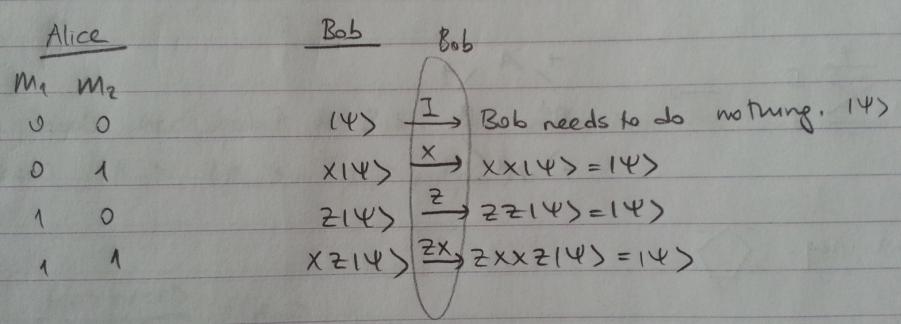
Teleportation'ın olması için Alice qubit'lerini ölçmeli. Ölçüm yapılan baz seti de Bell state'lerin baz seti olmalı. Alice'in yaptığı ölçüm haricinde uygulanan işlemler "üniter dönüşümler"dir. Bob'un en sonunda recovery işlemi için yaptığı dönüşümler, ölçüm değildir. Üniter dönüşüm matrisleri U olsun, measurement işlemi M olsun. State'e M'yi vurursan ölçüm, U'ları vurursan transformation yapmış olursun. Fiziksel olarak (deneysel olarak U nasıl bir işlemdir bilmiyorum). Bob'un recovery için ünitary transformation uygulaması operatör uygulaması demektir. Ölçüm yapmak da bir operatörle temsil edilebilir bence (Measurement operatörü); o zaman terminolojide operatör uygulamak demek ölçüm yapmaya tekabül etmez...

Literatürdeki teleportation senaryosu böyle. Ancak sen göndermek istediğin state'i, aldığın dolanık qubit state'ini ve sayısını, devreyi değiştirebilirsin amacına göre.

CNOT ve Hadamard'ı uygulama sebebimiz, ışınlanacak qubit'in kaysayılarını (alfa ve betayı) Bob'a ışınlamak. Bob'un elinde 0 ve 1'in süperpozisyonu olması yetmez; alfa ve betalı katsayılara sahip 0 ve 1'in süperpozisyonu olması lazım.


Bell Measurement

Yukarıdaki deneyde "linear evolution, local measurement" yapılmıştır. Linear evolution'da, detection apparatus, her parçacığa diğer(ler)inin state'inden bağımsız olarak etkimektedir. Local measurement'ta her parçacık belirli detector ile ölçülür.

Bell state measurement ise örneğin teleport edilecek 1 qubit, paylaşılan 1 EPR çifti olsun. Teleport edilecek qubit ile Alice'in EPR qubit'inin Bell state'lerin baz setine projective measurement yapılmasıdır. Alice'in elindeki 2 qubit'in hangi Bell state'e izdüştüğü bulunur. Bu, bağımsız iki kübiti dolanık hale getirir. A Bell measurement is an entangling operation. Bell state'ler entangled olduğu için Bell state bazlarına sahip bir baz seti ile ölçüm yapmak iki bağımsız qubit'i dolanıklaştırma işlemidir.

Bunun deneyi interferometreyle mi yapılıyor, deneyi nasıl yapılıyor? Bell state measurement 2 qubit'in beam splitter'dan geçirilerek enerjisinin yarıya inmesinin eşliğiyle ölçüm yaptığın baz setinin boyut sayısına ayrılmasıdır. Yani 4 boyutlu uzaysa dalga da 4'e ayrılıyor. 4 Bell bazı farklı açılarda görüntüleme perdesi koyulmasıdır. Parçacık veya dalga (hangisi) davranışı hangi aşamada olur? 2 qubit ya farklı deliklerden geçer ve dolanık hale gelmezlerse?

Joint state, teleport edilecek qubit ve entanglement'a sahip shared state qubit'lerinin tensör çarpımıdır. Anladığım kadarıyla Bell measurement, joint state'e single qubit gates (Pauli matrisleri, Hadamard gate) veya two qubit gates (CNOT) uygulamadan (yani bir devreye gerek duymadan) Bell measurement yapılarak qubit'in teleport edilmesi.


from computational basis to Bell basis

Deneysel olarak Bell state measurement uygulamak ve kapı dizisi uygulamak farklı şeyler olabilir. Ancak Bell state measurement'ın elle hesaplamadaki karşılığı, kapı dizisi uygulayıp joint state'in Alice'in qubit'leri kısmını computational bazlar cinsinden yazdıktan sonra computational bazlara teker teker H, CNOT uygulayarak Bell bazlarına geçmedir. Yani hesaplamada Bell state measurement'i taklit etmek istiyorsan yine kapı dizisi uygulayacaksın, ardından H(1) ve C(1)NOT(2) uygulayacaksın.

Std konu anlatımında dolanıklığı atlatmak için CNOT, H uygulanırken dolanıklığı geri getirmek için H, CNOT uyguluyorsun. Yani dolanıklığı hangi yöne ilerletmek istediğine göre sıra değişir.

Yukarıda psi2 durumunda 00, 01, 10, 11'in karşısında Bob'un qubit'inin halleri vardır. Bell state measurement yaptığında 00, 01, 10, 11 yerinde Bell state'ler yer alır. Hesaplamada joint state'in son hali, Bell state'ler cinsinden yazılır.



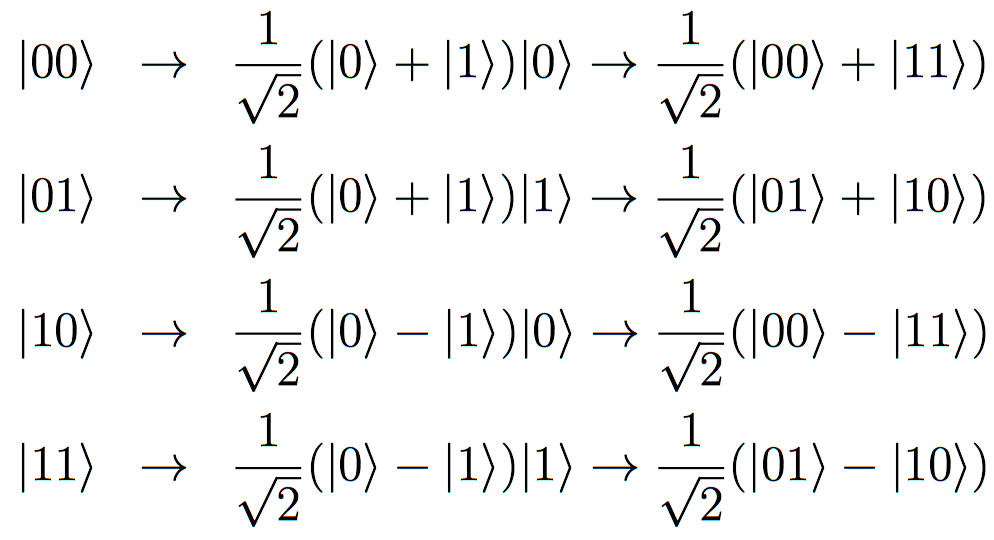
n qubit teleportation

  1. Teleport edeceğin qubit sayısı ne ise 2 katı sayıda qubit içeren quantum channel kullanılıyor.
  2. Teleport edeceğin qutrit sayısı ne ise 3 katı sayıda qutrit içeren quantum channel kullanıyorsun.
    Örneğin psi=a0+b1+c2 için GHZ=1/sqrt(3) 000+111+222 kullanıyorsun.
  3. Teleport edeceğin şey n boyutlu ise quantum channel'ın n adet aynı cins şey içeriyor.
  4. Teleport edeceğin state'in boyutu kaç ise ona göre dolanık state türü seçiyorsun.

Bir state'i generalized Bell states cinsinden yazmak

Generalize Bell basis of the Hilbert space of two qutrits:

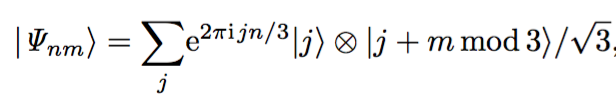
n,m,j=0,1,2

Bu formül ile, genelleştirilmiş Bell bazlarını elde ediyorsun.

Bir state'i generalized Bell basis cinsinden yazmak için, gereken yere cevabı birim matris olan complete Bell bazlarını yazmak gerekiyor. Yani o state'i Bell bazları üzerine izdüşürüyorsun. O bazlardaki ağırlık katsayılarını elde ediyorsun.

Alice, Bell bazlarında ölçüm yapıp psi00'ı elde ederse, Bob ve Charlie'nin qutrit'leri karşısındaki değeri; Alice psi21'i elde ederse BC'nin qutrit'leri karşısındaki halleri alır.


Local

Alice ve Bob ellerinde qubit'leri, farklı konumlarda iken (spatially separated) Alice'e göre kendi qubit'i local'de, Bob'taki local olmayan yerdedir.


Qutrit telenaklini qubit telenakline indirgemek

Arbitrary two-qubit basis are (00, 01, 10, 11). These basis have different coefficients as (a, b, c, d) respectively. Some symmetries can be defined on this two-qubit state: flip and exchange symmetries. Firstly, when we restrict our state to have exchange symmetry, basis 01 and 10 must have same coefficients. Take b=c. This is effectively a qutrit.

2 kübit durumunda b=c yanında bir de a=d alırsak efektif kübite dönüşür. a=d almamız da flip simetrisi gereğidir.

Şimdi kütritten başlayalım. Durumları (0, 1, 2) olarak etiketleyelim. Katsayıları (genlikleri) sırasıyla (a, b, c) olsun. Yukarıdakine benzeterek simetri kısıtı için burada a=c alalım. Sistem kübit görünümünde. (Kütrit halini matematiksel olarak indirgenmiş uzayda efektif bir kübit olarak yazabiliriz. Bir kütritin davranışını kübit gibi görebilmek için öyle bir observable seçilmeli ki bu observable kütritin o iki farklı durumunu birbirinden ayıramasın yani kütrit dejenere olsun.)

Kütrit telenaklini simetri kısıtı getirerek kübit telenakline dönüştürebiliyor muyuz bakalım. Daha sonra kübite has yazılmış telenakil protokolüne yakınsayıp yakınsamadığına, indirgenip indirgenmediğine bakalım. Bunun için 1-baştaki kübit hali, dejenere bazların genlikleri bakımından aynı mı bakılabilir. 2-ölçümde dejenere bazların ayırt edilip edilmediğine bakılabilir (yani dejenere bazların olasılıklarına bakılabilir).

Aşağıdaki örnekte, ikinci aşama sonuçlarında 2.durumda 2.bazın önüne kompleks sayı gelmiş durumda. Bu 0 ve 2 arasında oluşan relative faz, olasılık hesabı yapınca 0 ve 2'nin gelme olasılıklarını değiştirmiyor. Göndermek istediğim durumda da a2, 2.durumda da a2. Demek ki olasılık bakımından kübit hali, bu durumda korunmuş. Ancak 4.durumda dejenere bazın genliği ve olasılığı değişiyor. 1., 2., 3. durumlar hariç dejenerelik bozuluyor (dejenerelik bir 0'dan ayrılıyor bir 2'den ayrılıyor), kübit telenakline indirgenemiyor.


Peki 0 aynıyken 2'nin ve 1'in önüne sanal sayı gelmesi gerçek uzayda nasıl bir şeye tekabül ediyor?