Dalga Fonksiyonu & Operatörler
Gerçek uzaydaki fiziksel bir sisteme kuantum mekaniğinde dalga fonksiyonu karşılık getiriyoruz. Bu ölçekte çalışırken kuantum mekaniği postüla ve yasaları geçerli oluyor. Sistemin ölçülebilir özellikleri (konum, momentum, spin gibi klasik özellikleri) kuantum mekaniğinde Hermitik (conjugate transpose'u kendine eşit) operatörlerle ifade edilir. Özdeğerleri reeldir. Ölçülebilir büyüklüklere observable'lar denir. Operatörler; eigenvalue'ları ve
eigenfunction'ları ile tanımlanır. Eigenvalue'ları bulmak için aşağıdaki denklemi kullanıyoruz:
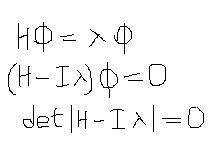
Bu denklemle \(\lambda\)'ları bulduktan sonra eigenfunc.ların bulunmasına sıra geliyor:
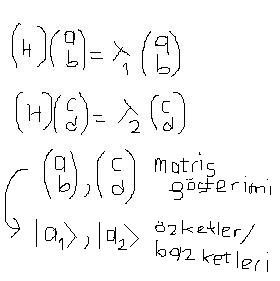
Dejenere olmayan durumlarda eigenvalue sayısı kadar eigenfunc. vardır. Eigenfunc sayısı uzayın boyutunu belirler. Yukarıdaki 2D-space idi.
Sistemin bir karakteristiğine ait dinamik, bir matris olarak yazılır; örneğin öteleme operatörü, konumu evriltir. Örneğin konum operatörünü duruma vurursun ve konum operatörünün özdeğerlerinden birini elde edersin. Tüm iki (ya da n) seviyeli sistemlerin örneğin konum, momentum operatörleri aynı değildir. Peki bu operatörler nasıl bulunur?
"İki seviyeli sistemlerin mekaniği sigma x,sigma y,sigma z (Pauli X,Y,Z) ile belirlenir." ifadesi yanlışmış. (Newton mekaniğinde kinematik, sistemin hareketini yani zaman evrimini inceler; dinamik buna ek olarak sebeplerini inceler.) Kuantum mekaniğinde dinamik sistemin zaman evrimini inceler. Bir sistemin, kendisine \(\hat{U}(t,t_0)=\exp{(-i\frac{\hat{H}(t-t_0)}{\hbar})}\) unitary time evolution operatörü vurularak zaman evrilmesi sağlanır. 2 seviyeli bir sistemin dinamiği, Pauli spin operatörleri ile bulunmaz. Pauli operatörleri sadece spin observable'ına ait operatörlermiş. Pauli operatörleri başka işe yaramazmış. Bir operatörü bir ket'e vurmak, ölçüm (measurement) yapmak değildir.
Ancak ölçüm yaparsan ne elde edeceğini görmek olabilir. Pseudospin operatörleri, sadece ve sadece spin gözlenebiliriyle ilişkili o zaman. Fotonun spini 3 seviyelidir. Ya da n seviyeli sistemler. Hepsi Pauli op.larının genelleştirilmiş hali. O zaman adı neden pseudo? Neden exact/absolute/for sure değil?
Dejenerasyon
Bir operatörün (sistemin konum gibi bir karakteristiğinin ya da Sz gibi spin karakteristiğinin bir doğrultusunun (z bileşeninin)) özdurumları uzayı tarar. Her özduruma karşılık bir özdeğer vardır. Özdeğer ve özdurum, belirli bir sonuca/duruma has ikilidir. Örneğin bir elektronu manyetik alana koyduk ve sapmasını ölçtük. Sapma, elektronun spin durumunu verir. Bir doğrultu seçtik, bu doğrultuya Sz operatörünü karşılık getirdik. Sz'yi elektronun durumuna vurduğumuzda/ölçüm yaptığımızda yukarı giderse "spin-up", aşağı giderse "spin-down" dedik. Spin-up |0> özdurumuna, spin-down |1> özdurumuna karşılık gelsin dedik. Yukarı yön +, aşağı yön -'dir. Elektronun spin açısal momentum değeri olan hbar/2 Joule*saniye ile birlikte |0> özdurumuna karşılık +hbar/2 özdeğer atadık. |1> özdurumuna da -hbar/2 özdeğerini atadık. Belirli operatör için özduruma karşılık unique bir özdeğer vardır. Ancak dejenere durum, özduruma karşılık unique özdeğerin belirlenememesidir. Yani birden fazla eigenvector'un eigenvalue'su ortaktır. Aslında elektronun saptığı yönü görsek özdeğeri atayacağız ancak özdurum/özdeğer ayırdına varılamadığı için dejenere durumları belirlemede birden fazla kuantum sayısı kullanılır.
Klasik laf: Ölçüm yaptığımızda bir özdeğer elde ederiz. Özdeğer ölçüm sonucumuzdur. Sistemin çöktüğü durumsa özdurumdur. (Bence özdurum da özdeğer de aynı duruma işaret eder. Aynı şeyi iki kere söylemek gibi gereksiz.)
Bir dalga fonksiyonunu operatörün özketleri tabanında yazarsak dejenere özketlerin olasılık genlikleri aynı olmak zorunda mıdır: Hayır.
Dejenere özketler, birbirine dik olmak zorunda değiller.
Dejenereliği matris üstünde görelim
Elimizde diagonalize matris olsun. Köşegenler eigenvalue'lardır. Aşağıdaki matriste iki adet lineer bağımsız eigenfunction (baz) dejeneredir, eigenvalue'ları 2'dir:
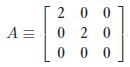
2 katlı dejenerelik vardır. Dejenere durumlar (1,0,0) ve (0,1,0) dır.
Bu eigenfunc.lar lineer bağımsızdır; lamda'ların birbirine göre özelliğinden dolayı. Eigenfunc.lar birbiri cinsinden yazılamaz, dolayısıyla uzay oluşturup uzayı tararlar (span the space) ve uzayın basis set'ini (orthogonal set) oluştururlar. Wavefunc.ımızı, bu eigenfunc.larla ifade edebiliriz (an'ler olasılık genlikleri):
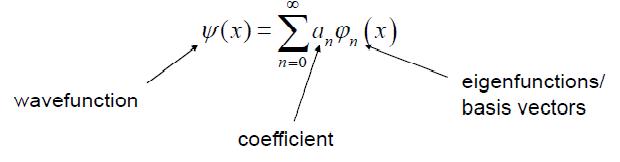
Operatöre göre farklı basis set'ler ile uzay oluşturup wavefunc.ı farklı eigenfunc.larla yazabiliriz.
Be aware of:
Operatörün eigenfunc.ları ile uzay oluşturuyorsun. You can pop up many spaces by calculating / determining eigenfuncs of different operators. Still there is no wavefunc on them. These are empty spaces without wavefuncs. You put your wavefunc onto any space.
Tam bu noktada: Bir wavefunc'ı aynı anda tüm uzaylarda yazamayabilirsin. Çünkü wavefunc'ı yazmak için ölçtüğünde onu çöktürürsün. Halbuki ölçümden önce wavefunc o durumda olmayabilir. Ve farklı bazda bir wavefunc'ın nasıl davranacağını bilemezsin. Ancak aynı eigenfunc'lara sahip (aynı basis set ile yazılabilen) operatörler eş zamanlı ölçülebilir. Eş zamanlı ölçülmek de commute etmektir.
- A ve B operatörü commute ediyorsa,
- A'nın eigenfunc'ları dejenere değilse,
- Ölçülebilirler (fiziksel sonuç veren op.lar) Hermitseldir. Hermitik op.lar diagonalize edilebiliyordur.
- B de aynı eigenfunc'larla diagonalizedir.
- Yani A diagonalken B de diagonaldir (köşegendir). Yani özdeğerleri aynıdır.
- Çünkü diagonal elemanlar özdeğerlerdir.
- Dejenere olma ve Commute et
Her observable, diagonal matrix olabilecek bir bazda yazılabilir. Aynı observable'ın diagonal bazda yazmak kanonik formda yazmaktır. Diagonal ve diagonal olmayan bazlar arasındaki dönüşüm kanonik dönüşüm mü oluyor dolayısıyla? Bu observable konum operatörüyse x-uzayında ifade etmekten p-uzayında ifade etmeye geçmek gibi mi oluyor? Buradaki baz setinin cinsini değiştirmek: x'ten p'ye.
Ayrıca grup teorisinde diagonalize etmekle ilgili vardı bir şeyler...
Komüte eden operatörler 2 çeşit
Komüte eden operatörler, aynı parçacığın üzerinde aynı anda ölçülebilen operatörler olabilir ya da farklı parçacıklar üzerinde işlem yapan operatörler olabilir.
\([S^2,S_z]=0.\) \(S^2\) ve \(S_z\) operatörleri aynı parçacığın spin uzayı üzerinde ölçüm yapıyor.
\([S^2_1,S^2_2]=0\) Sırasıyla 1. ve 2. parçacık üzerinde işlem/ölçüm yapıyorlar.
Birincisinde uzayı tam tanımladık, dejenereliği kaldırdık (\(\sum_i{\ket{n l m}_i}{\bra{n l m}_i}=\mathbb{I}\) tam cümle, yani her şeyi \(S^2\) ve \(S_z\)'nin eş zamanlı özdurumlarıyla (\(\ket{n l m}\)'lerle) ifade edebilirsin). İkincisinde \(S^2_1\) ve \(S^2_2\)'nin işlem yapacağı bir uzay tanımladık. Dış çarpımla uzayı büyüttük. Her iki durumda da elimizde 1 adet uzay var diye düşünebiliriz. Yani komüte eden operatörler, ya aynı parçacık üzerinde aynı anda ölçülebilen büyüklüklerdir ya da tamamen farklı uzaylardaki operatörlerdir.
- Operatörün eigenvalue'ları operatörün hangi bazda yazıldığından bağımsızdır.
- Bir operatörü bir durum üzerinde ölçmek demek, hangi eigenvalue'ların hangi olasılıkla bulunduğunu tespit etmek demektir. Bunu yapmanın yolu, bir eigenvalue'ya karşılık gelen eigenfunc.ı o durum üzerine izdüşürmektir: Bra eigenfunc ile ket durumu çarpımı yapılır:
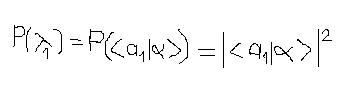
Ek 1:
İzdüşürmek, eş olmayan uzaylar arasında yapılamaz. Bizim uzaya eş uzay, U dönüşüm matrisiyle benzerlik dönüşümü yapılarak yaratılan yeni uzaydır. Benzerlik dönüşümü, bizim uzayı geren her baz için (yeni) eş baz yaratmalıdır. Boyut kaybı olmaması gerekir, eş uzaylar aynı boyuta sahiptir. Örneğin biri 2D biri 3D olamaz.
2 eş uzay arasında dönüşüme uğrayacak matris (yani iki eş uzayda da aynı özdeğeri verecek matris - zaten özdeğerler uzay seçiminden bağımsızdır dedik) (yani sistemin ötelemeler ya da dönmeler altında korunan büyüklüğü) 3x3'lükse eş matris de 3x3'lük olmalıdır.
Spin uzayındaki Sx+, Sx- uzayından Sy+, Sy- uzayına veya Sz+, Sz- uzayına dönüşümler benzerlik matrisiyle yapılır. Bu uzaylar birbirlerine göre 90 derece döndürülmüş uzaylardır. Eş uzay; döndürme, öteleme ile yapılıyor.
3 boyutlu bir durum üzerine 2 boyutlu spin uzayını izdüşüremezsin. Önce durumunu spin uzayında yazarsın, ardından spin operatörünün eigenfunc.larını izdüşürürsün, böylece neyden ne kadar var görürsün
(spin op.unun eigenvalue'larından bizim durumda ne olasılıkla var görürsün).
Sx, Sy, Sz spin operatörlerinin yanlarına i, j, k birim vektörlerini koyarak S vektörünü elde edebilirsin (S=Sxi+Syj+Szk). Çünkü Sx operatörü x doğrultusundaki nesne üzerinde işlem yapan operatördür, bunu vektörleştirebilirsin. Operatör bir matristir, matris denklemler setidir, set çözülerek bir vektör olabilir. Biz denklem setini çözmeden vektörleştirip işleme sokuyoruz.
Üniter Benzerlik Dönüşüm (Unitary Similarity Transformation) (Unitary Transformation)
Üniter benzerlik dönüşüm
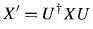 formülü ile yapılır.
formülü ile yapılır.
-
X eski uzaydaki hareket sabiti (örneğin Hamilton).
- X': yeni uzaydaki aynı büyüklük.
- X matrisi U ile dönüşüyor, uzayın baz vektörleri de aynı U ile dönüşüyor.
- U üniter bir operatör. In QM a unitary operator is associated with an operation like translation or rotation. U has become a symmetry operator.
- X'in üniter olarak eşdeğer işlemcisi X' 'dır.
- Üniter olarak eşdeğer işlemcilerin spektrumu (özdeğerler cümlesi) aynıdır. Zaten özdeğerler uzay seçiminden bağımsızdır dedik.
- Üniterlik: UU+=U+U=1. Üniterlik tersinirlikle ilgili. UU+ yaptın mı gittin geldin demektir. Ya da periyodik bir hareket var gibi. Group theory'deki cyclic group gibi. Bu arada Quantum Fourier Transformation'da da bir cyclic'lik var: Go to QFT page Tersinir: invertible or reversible
- Hermitlik: p=p+=p-1
Örnek: 2 tane boson türünde identical particle düşün. Initial position ve final position'ları olsun. Initial'dan final'a gelirkenki trajectory'lerini çıkaramadığımız için (Bunun sebebi enstrument hassaslığının düşük olması değil işin doğasının bu olmasıdır. Sanırım parçacıklar multiverse'de hareket ettikleri için sadece universe'te ölçüm yapan bir aletle ölçüm yaptığımızdan teşhis edemiyor değiliz. Yani bir gün multiverse'te ölçüm yapan enstruments geliştirilebilirse trajectory çıkaramayabiliriz. Sanırım parçacıklar gözlenmediğinde tüm durumlarda birden oluyorlar. Zaten multiverse'te ölçüm yaptığında tüm durumları tek bir zaman için elde edersin. Aynı t anı için bu universe'te bu değeri alıyor, şu universe'te şu değeri alıyor dersin sanırım. Bunu demek trajectory çıkarmak olabilir de olmayabilir de. Trajectory'nin tanımı değişebilir bu durumda.) hangi particle hangi final position'a geldi bilemiyoruz. Bunların H'si simetriktir (Hamilton hareket sabiti). Parçacıkların final konumlarını değiştirmek 2 eş uzaydan bahsetmektir.
2 özdeş parçacık fermion olsaydı final konumlarının değiştirilmesi altında dalga fonksiyonları antisimetrik olurdu. Yine "Hamiltonian is invariant under interchange of particles." der miydik? Go to Permutation Symmetry for Identical Particles
Gelelim U'nun eldesine
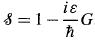
Yukarıdaki formül diyor ki simetri operasyonları (S) (öteleme/dönme operasyonları), identity transformation'dan (\(\mathbb{I}\)'dan) sonsuz küçük derecede değişimle tanımlanır. \(\varepsilon\): sonsuz küçük öteleme (S, bu parametreye bağlı). G: Simetri operasyonunun hermitik jeneratörü (hermitian generator). And if H (Hamiltonian) is invariant under S (H, S dönüşümü altında invariant'sa):
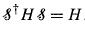
Simetri/dönüşüm operatörünün ötelemelerdeki karşılığı:
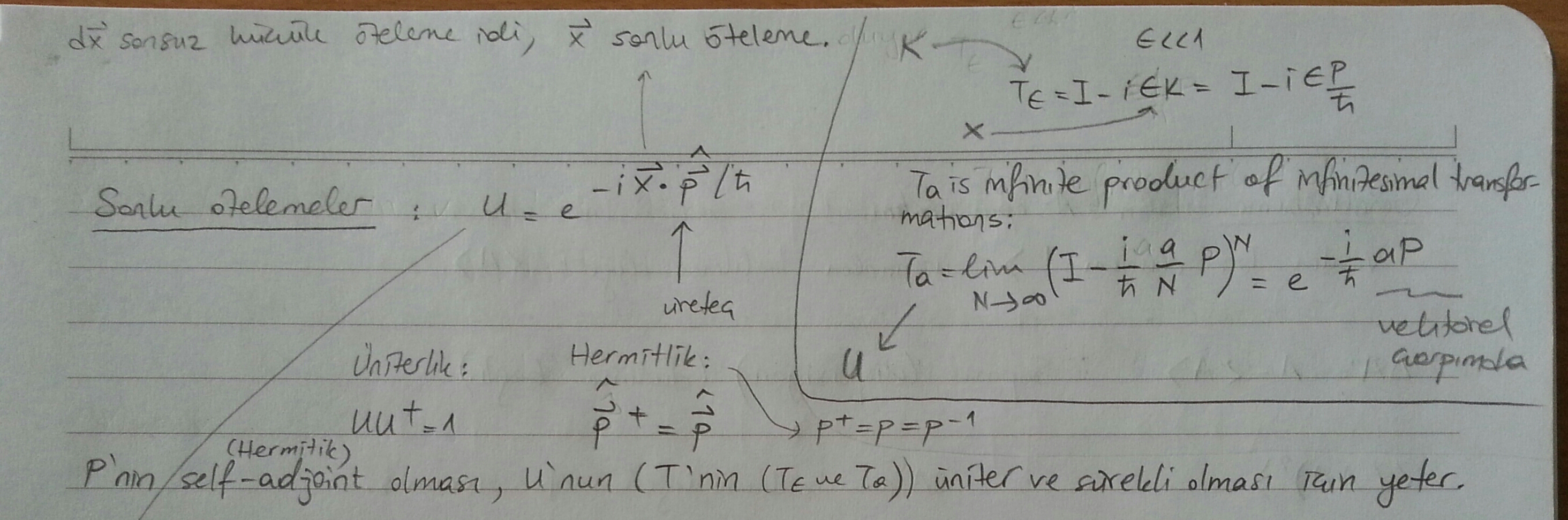
Burada momentum, ötelemenin jeneratörü. Infinitesimal transformation'dan finite transformation'a geçiş.
Üniter Benzerlik Dönüşümüne Örnek
Özdeğer problemi, bir matrisi diagonalleştirerek özdeğerlerinin diagonalde bulunduğu formu elde etmektir. Bu da matrise karşılık gelen büyüklük için eş uzay yaratmaktır. Eigenvalue probleminin çözümü buradan çıkmıştır.

Bu eigendecomposition of matrix'tir.
Benzerlik Dönüşümü (Similarity Transformation) (Nonunitary Transformation)
In this case, the transformation operator is not unitary.
Gram-Schmidt Transformation (Nonunitary Transformation)
In this case, an operator which is written in nonorthogonal basis is transformed to the representation in orthonormal basis. Upper or lower triangular matrices are the results of this transformation.
Nonorthogonal basis \(\longrightarrow\) orthonormal basis
Simetri operatörü ile sistemin korunan büyüklüğü komüte ediyor. (Simetri operatörü: dönme veya öteleme. Üniter bir işlem. Yani ket'in boyunu değiştirmeyen bir işlem. Üniterliğin sebebi, etkidiği ketin boyunu değiştirmemek. \(U \ket{\alpha}\) iken \(\bra{\alpha}U^\dagger U\ket{\alpha}=\braket{\alpha}{\alpha}\) olsun. \(\Rightarrow U^\dagger U=\mathbb{I}\) )
\(S^\dagger HS = H \hspace{1cm} \Longrightarrow \hspace{1cm} HS=SH \hspace{1cm} \Longrightarrow \hspace{1cm} [S,H]=0\) Komütasyonu sıfır.
Parite altında konum operatörü X, eksilisine gidiyor.
\(\Pi^\dagger X\Pi=-X \hspace{1cm} \Longrightarrow \hspace{1cm} X \Pi=-\Pi X \hspace{1cm} \Longrightarrow \hspace{1cm} {\Pi,X}=0\) Antikomütasyonu sıfır.
Tek parite varsa antikomütasyon var, çift parite varsa komütasyon var.
Simetri operatörü olarak dönme operatörünü (D(R)) alalım (D(R): Klasik olarak R dönmesine karşılık gelen işlemci). Sistem Hamilton ile verilsin. Sisteme dönme operatörünü uygulayalım.
\(H \ket{n}=E_{n}\ket{n} \\
SH\ket{n}=S E_{n} \ket{n}=E_{n}(S\ket{n})=H(S\ket{n})\) Demek ki \(E_{n}\) hem \(\ket{n}\)'nin hem \(S\ket{n}\)'nin enerjisi. \(\ket{n}, S\ket{n}\) birbirine dik, ortogonal, lineer bağımsız özdurumlar. Çünkü \( S\ket{n}\) aslında farklı m değerine karşılık gelen durumdur. D(R), belirli j değeri için m'ler arasında döner, m'ler arasında geçiş yapar. Ama enerji m'lerden bağımsızdır, hatta j'lerden bağımsızdır, n'lere bağlıdır.
Ek 2:
Döndürmek bir vektöre faz eklemek ile ilişkili. Döndürmek fiziksel ölçümün sonucunu değiştirmez.
\(\ket{\alpha} \rightarrow e^{i \theta}\ket{\alpha} \\ e^{i \theta}\): faz faktörü
Bilmiyorum: Dalga fonksiyonu ışındır. Bir yönü vardır. Eksi ile çarpmak yönünü değiştirir. Kompleks sayı ile çarpmak döndürmez, reel bir sayı ile çarpmak boyunu değiştirir. (?)
Yukarıdaki ifade belirli enerji seviyesinde bulunan bir sistemin farklı gözlenebilirine ait bazlar olabilir. (Bazlar farklı özdeğerlere sahip olur örneğin.) Bu gözlenebilir, enerji bakımından dejenere uzay oluşturur. Gözlenebilirin tüm değerleri, belirli enerji seviyesinde görülür. Ya da yukarıdaki ifade, farklı enerji seviyelerinde bulunma olasılık genlikleri olabilir. Burada enerji bakımından farklı özdeğerlere tekabül eden özdurumlar toplanıyordur. İlki yatayda toplam gibi, ikincisi düşeyde toplam gibi. İkincisinde dejenerasyon yok, ilkinde bir gözlenebilire göre dejenerasyon var.
SANIRIM: Quantum number'lar orbital'leri niteler. s,p,d,f diye gittikçe uyarılmışlık artmaz, quantum number arttıkça uyarılmışlık artar. Örneğin n'ler 0'dan başlasın; n=0 ground state, n=1 1.uyarılmış durum (first excited state), n=2 2.uyarılmış durum. Örneğin s ve p orbitalleri aynı uyarılmış durumda bulunabilir. Basis'lar o kuantum durumundaki elektronun wavefunc'ının belirlenmesi için olan bilinmeyen parametrelerdir. Basis set, parametre seti. Uzay dediğimiz şey, bir baz seti cinsi (bu setin döndürülmüş halleri farklı uzay oluşturmaz ama. Yani bir operatörün diagonal ve nondiagonal halleri aynı uzaydır.

Operatörü wavefunc.a vurursun. Vurmadan önce operatörün (ölçmek istediğin büyüklük) kendi özvektörleri (eigenvector/eigenfunction) tabanında ifade edilmişse bu operatörü wavefunc.a vurduğunda elde edeceğin sonuç, operatörün eigenvalue'larından biri olacaktır. Ama operatörü vurmadan önce kendi eigenvector'leri bazında yazmamışsan eigenvalue'lardan birini elde etmezsin. Bu arada ölçüm yaptıktan sonra elde ettiğin sonuç, operatörün yazıldığı bazda wavefunc.ının bulunma katsayılarıdır. Bu katsayıların karesi, ölçüm sonunda dalgafonk.unun o bazda bulunma olasılıklarıdır. (Bir operatör kendi özvektörleri bazında diagonaldir.)

Eigenfunctions are stationary
states. So basis set is stationary states. And for time dependency just add an
exponential part to stationary states. Time part shows how positions will
evolve in time.
Orthogonality

Denklemin yorumu: farklı eigenfunc.ların kesişiminin coord. ekseniyle arasında kalan alanların toplamı sıfırdır. Çünkü func.ların/baz vektörlerinin kesişimi bir noktadır, noktanın izdüşümü alan kaplamaz.
Operatörü yine eigenfunc.a vurmuş, anlaşılan wavefunc.a vurmuyorsun!!?
Stern-Gerlach Experiment
Deneyde gümüş atomu (Ag) kullanılmış.
Ag'nin 47 elektronu var. 46 elektron shell'lerde (quantum states'te) tüm orbitalleri dolduruyor. 47.elektron, 5s orbitalinde 1 adet elektron yeri doldurabiliyor. Bu son orbitalde (outer shell) unpaired electron oluyor.
Tüm orbitalleri dolmuş shell'ler/paired electron varlığı için sıfır net açısal
momentum söz konusu. Unpaired electron bulunması/boş orbital bulunması net açısal momentum yaratıyor. Simetri bozuluyor, açısal momentum varlığı tespit ediliyor. Açısal momentum kesirli çıkıyor. L (orbital angular momentum) tam sayı değer alır, S (spin angular momentum) kesirli değer alır. Dolayısıyla açısal momentumun spin kaynaklı olduğu keşfediliyor (L+S).
Nucleus spin'e (I) girmedik!?
s,p,d,f'nin katsayıları n quantum number'lardır. s, p, d, f'nin kendisi de açısal momentum kuantum sayısı l'nin değerini belirler. l=0,1,2,3,4 sırasıyla s,p,d,f,g'ye denk gelir. n temel kuantum sayısı. Açısal momentum kuantum sayısı l=0,1,2,...,n-1. Açısal momentumun z bileşeni m=-l,...,l. n,l,m olarak 3 kuantum sayısı vardır. Bunlar tamsayı alır.
s --> l=0
p --> l=1
d --> l=2
f --> l=3
g --> l=4
S, L ile aynı cebri gösterdiği için spin, açısal momentumdur diyoruz:
L2=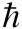 2 * l(l+1)
2 * l(l+1)
S2=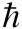 2 * s(s+1)
2 * s(s+1)
Spin: fixed & independent
- Spinin özdurumları fonksiyon değildir; eigenfunc diye adlandıramayız; ancak eigenvector ya da eigenstate diyebiliriz. (Eigenstates are not functions. That's why we use ket notation.)
- Eigenstate diyoruz fakat quantum state'le karıştırılmasın, parçacığın hangi
quantum state'te olduğundan bağımsız olarak sabitler.
- Spatial wave func. ile outer product yapıyoruz. Schrödinger denkleminin çözümüyle sadece wavefunc elde ederiz. O zamanlar spin keşfedilmediği için Schrödinger denklemi çözümüne dahil olamadı. Ancak spatial wavefunc ve spin farklı uzaylar oldukları için belki yine dahil olmayacaktı.
- S2'nin ve Sz'nin eigenvector'leri:
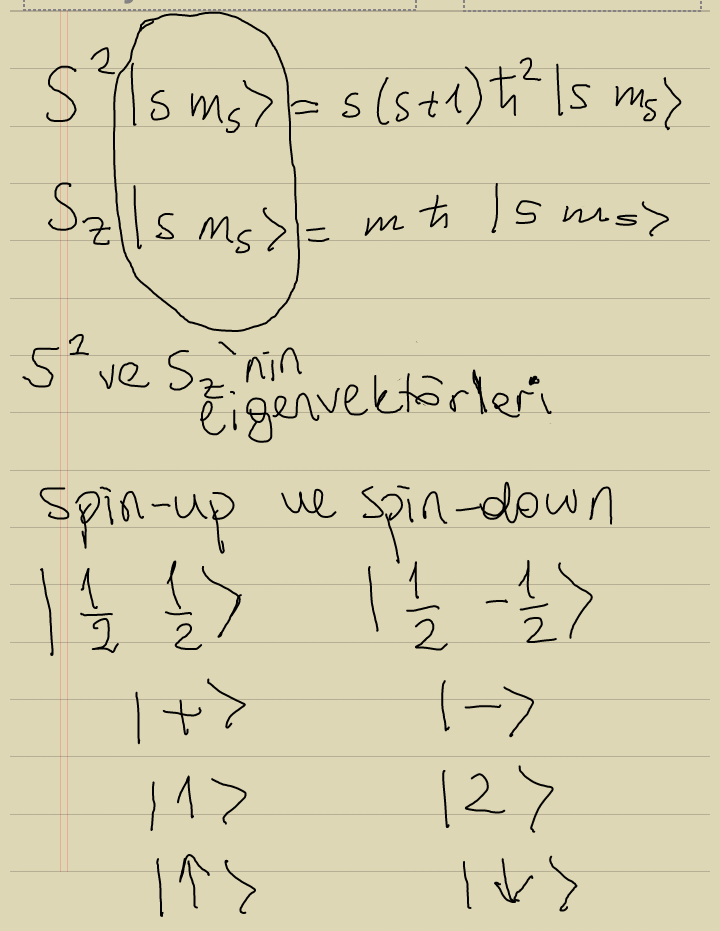
Beklenen Değer
Bir operatörün/ölçülebilirin beklenen değeri için wavefunc'ın cc'si ve kendisi arasına sandviç yapılıp operatörün istenen domain'de de integrali alınır:
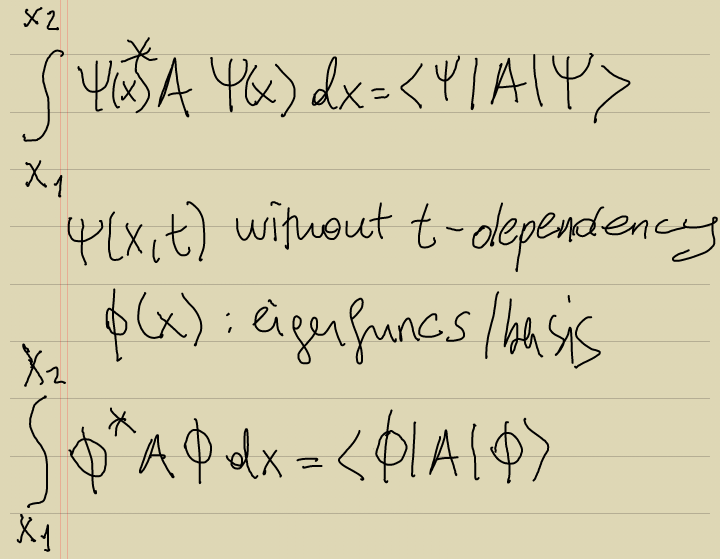
Burada
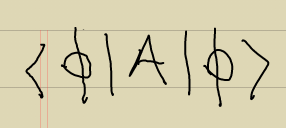 ifade aslında A'nın matris temsilinde ij'inci elemanıdır:
ifade aslında A'nın matris temsilinde ij'inci elemanıdır:
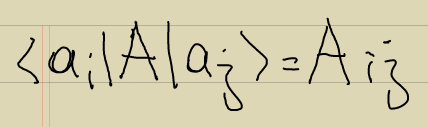
A op.u (bir fiziksel değer) ölçüldüğünde bulabileceğim değerler ai'ler (bizim fonk.un o bazda yazımının katsayıları) ile verilir. ai'lerin olasılığı
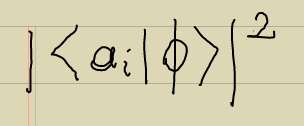 ile orantılıdır.
ile orantılıdır.

Kavramsal olarak: Bir şeyin beklenen değeri için sandviç yapıyorsun. Bu mutlak değer karesini almaya tekabül ediyor. Aradığın şey durumunu/wavefunc.ını etkilemiyorsa sandviç dışına çıkıyor ve A op.unun özdeğerlerine karşılık gelen özdurumlarının bizim durumda/wavefunc.ta ne oranda bulunacağına dönüşüyor. Problemler farklı sunuluyor ama alttaki işlem (yaptığın şey, aradığın şey) aynı. Yani bir gözlenebilirin beklenen değeri ile bir gözlenebilirin özdeğerine karşılık gelen özdurumlarının/fonksiyonlarının bizim durumda bulunma olasılıkları aynı problemdir!
Belirli eigenfunc'ın bulunma olasılığını bulmak, o eigenfunc'ın ağırlığını bulmak gibi, ağırlıklı değer bulmak gibi. Beklenen değer almak da ağırlık bulmak gibi. Ama bu tam olarak "ağırlıklı ortalama" alma kavramına tekabül ediyor mu bakmak lazım.
Bir op.un belirli eigenvalue'sunun bir durum üstünde bulunma olasılığını bulmakla bir op.un beklenen değerini bulmak (ortalama almak) arasındaki fark, beklenen değerde eigenvalue'lara karşılık gelen bazlarda
(sanırım bu baz, op.un matrisini çaprazlayan bazdır, yani diagonalleştiren
bazdır. Op.u diagonalleştirirsin ki eigenvalue'ları elde edebilesin) sistemin bulunma ağırlıklarını topluyorsun. Diğerindeyse tek bir eigenvalue'nun ağırlığını buluyorsun.
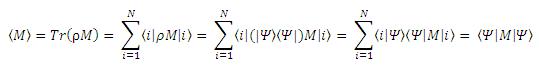
Density matrix'te pure state'in ortalaması (trace'i) 1, mixed state'in 1'den
küçük. Ama operatörün beklenen değerinin 1'den küçük veya eşit gibi bir sınırı
yok. Pure state'in density matrix'inin eigenvalue'ları toplamı 1'e eşittir. Bu
toplam, trace almaktır. Operatörün eigenvalue'ları çaprazlayan bazda diagonalde
bulunur ama eigenvalue'ların toplamı (operatörün ortalaması) 1 ile kısıtlı
değil. Op.un beklenen değeri bir sistem üstünde ölçüm yapılarak bulunur ama eigenvalue'ların toplamı için baza ya da sisteme ihtiyaç yoktur. Burada sorun yok ama eigenvalue'ları ister baz setine yerleştir topla ister yerleştirmeden topla.
Yukarıdaki örnek kesikli eigenfunc ve eigenvalue için yazıldı. Sürekli spektrum olsaydı kronecker deltası kronecker delta fonksiyonuna dönüşecekti. O da fonk içini sıfır yapan noktada integral sonucunu 1 verir:
Netice: Bir durum üstünde bir operatörün, özdeğerlerinin bulunma olasılığı birer boyutta bulunma durumunu verirken beklenen değeri tüm boyutlardaki bileşenlerin vektörel toplamını verir.
Uzayı Germe/Tarama
[x, px]= i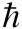
[y, py]= i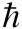 (sıfırdan farklı değer)
(sıfırdan farklı değer)
[z, pz]= i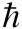
Aynı eksen üstünde x ve p'yi eş zamanlı ölçemezsin. Çünkü uzayı germezler. Birbirlerine bağımlıdırlar. Bağımlı olduklarını iki şekilde görebilirsin:
- p=mdx/dt Yani p değeri x'e bağlı. Lineer bağımsızlık benzetmesiyle bağımsız değiller. Bağımlı, bağımsız kavramını benzerlik ile gördük.
- p dalga üstünde ölçülürmüş, dalganın p'sini ölçersin. Konum ölçmek için parçacık üstüne foton yollarsın ve etkileşime girer ve çöker; p, hız kalmaz... Demek ki parçacık çökeceği için p'yi parçacık üstünden değil dalga üstünden ölçermişsin. p'yi nasıl dalga üstünden ölçeriz?
[x, py]= 0
[x, pz]= 0
Farklı eksenler üstünde x ve p'yi eş zamanlı ölçersin ama!
Çünkü x ile py uzayı gerer! (Lineer bağımsız eksenler üstünde iş yapıyorsun. Gerer dedim ama aslında üzerinde çalıştığım eksenler gerer.)
Not: Peçete gerilimi. Üçgen peçete olur, beşgen, dokuzgez olur. Germeyi ve multi boyutları böyle de düşünebilirsin.
Density Matrix
ro'yu sigma z üzerine izdüşürmek, sigma'nın belirli yöndeki bileşenini almak gibi.
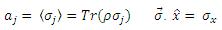
Photon polarization degrees of freedom
Fotonu biz hazırlamadıysak polarizasyon tipini (linear, circular, elliptical polarization) ölçmeden bilemeyiz. Fotonun polarizasyon serbestlik derecesi, polarizasyon tipi ne olursa olsun boş uzayda 2'dir.
Bir dalga boyunun ilerleme hızı faz hızını verir. Yani dalga ilerlerken dalganın başlangıç noktasının dalganın bitiş noktası ulaşması için geçen sürede kattettiği yoldur.
Faz açısını ilerleyen dalga şekli üstünde çizemeyiz, ancak hesaplayabiliriz.
Dalgayı \(A\cos{(\omega t-k x)}\) olarak yazalım 1 boyutta. \(\omega t-k x=\phi\): faz açısı
\(\cos{\phi}=\cos{(n\pi)}\) olarak sabitleyelim dalgayı. Bu sabitleme faz hızının sabitlenmesinden geçer. Yani \(\frac{d\phi}{dt}=0\) olmalı.
- \(\frac{d\phi}{dt}=0\)
- \(\frac{d(\omega t-kx)}{dt}=0\)
- \(\omega t=kx\)
- \(\frac{x}{t}=\frac{\omega}{k}\) faz hızıdır.
Fotonun boş uzayda polarizasyon serbestlik derecesi sayısı 2'dir: u ve v. Bu 2 bileşen şuradan gelir:
- \(\vec{\nabla}\times\vec{A}=\vec{B}\)
- \(\vec{A}=\vec{A}(A_x,A_y,A_z)\)
- \(\vec{A}\) 3 bileşene sahip.
Ama boş uzayda dalganın ilerleme yönünde (\(\hat{k}\)) alan yok, dolayısıyla vektör potansiyel alanı da yok: \(A_z=0\). Dolayısıyla 3 boyuttan 2 boyuta iner.
Polarizasyon, dalganın elektrik alan vektörünün doğrultusundadır. \(\vec{E}\times\vec{B}=\hat{k}\) .\(\vec{E}\)'nin 3 değil 2 bileşeni vardır: u, v. Kaynak noktamız \(\vec{A}\) olduğu için 2 bileşenin kaynağını \(\vec{A}\)'ya bağladık.
OfAWave.png)
\(\vec{B}\), \(\vec{A}\)'nın curl'üne eşit. \(\vec{B}\) de \(\vec{A}\) da rotasyon hareketi yapıyor. Circular ve elliptical polarization'da \(\vec{B}\) döner, linear polarization'da dönme hareketi yapmaz. O zaman \(\vec{B}\)'nin \(\vec{A}\)'ya bağımlılığı nasıl olur?
Foton, bir spin-1 parçacığıdır.
\(s=1\)
\(\vec{S}\): Spin açısal momentumu
\(\vec{S_z}\): Spin açısal momentumun z bileşeni
\(S_z=m_s\hbar\)
\(m_s=-s,..,+s=-1,0,+1\)
\(S_z\)'nin özdeğerleri -1, 0, 1.
\(\vec{S_z}\), fotonun ilerleme doğrultusunda olan vektör.
\(S_z\)'nin özdeğeri 1 ise left hand circular/elliptical polarization.
\(S_z\)'nin özdeğeri 0 ise linear polarization.
\(S_z\)'nin özdeğeri -1 ise right hand circular/elliptical polarization.
\(\psi_{nlm}\): konum uzayı.
\(\chi_+, \chi_-\): spin uzayı.
Overall wavefunc=spatial \(\otimes\) spin
Overall wavefunc=Angular momentum of light
Overall wavefunc=Orbital angular momentum \(\otimes\) Spin angular momentum
Overall wavefunc =wave fronts \(\otimes\) polarization
\(\otimes\), vektörel çarpım değil, dış çarpımdır.
Foton için spin, kendi ekseni etrafında dönme, elektrik alanın dönmesidir.
Parametric Down-Conversion (Source of entangled photon pairs)
Composite system, birden fazla sistemin birleşimi demektir. Yöntem olarak subsystem'lerin tensor product'ı ile yazılır ancak individual subsystem'lere ayrılabilir şekilde yazılabiliyorsa composite sistemin separable'dır, ayrı sistemleri tek başlarına ifade edemiyorsan composite sistemin entangled state'tedir.
An optical component is said to be linear if its output modes are a linear combination of its input modes. Yaratma, yok etme operatörleri cinsinden gösterelim. Aşağıda ak+ girdi modları, bj+ çıktı modu.
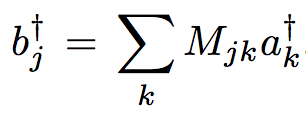
Calsite crystal'e gelen ışın composed system'dir: polarization vs location of path (2 degrees of freedom)'in tensor product'ıyla yazılabiliyor. ("Location of path", "spatial mode", "two eigenfunctions of angular momentum" aynı karaktere ait kavramlar.) (Aşağıdaki örnekte 1 fotonun kristalden geçtikten sonra ortaya çıkardığı 2 fotonun path'lerinin lokasyonu farklı. Ayrıca momentum vektörlerinin yönleri farklı. Ya momentum farklılığından dolayı 2 foton farklı uzaysal modda demektir ya da çıkan 2 fotonun lokansyonları farklı Hilbert space'e ait olduğundan.) (Burada momentum angular momentum olarak geçebiliyor. Frekans, angular frequency olarak geçebiliyor. Buradaki açısallığı bilmiyorum, neden açısal? Frekans bilgisine polarization degree of freedom'dan da spatial degree of freedom'dan da ulaşılabilir. Çünkü frekans enerjiyle ilgili. Elektrik alanın şiddeti, ışının enerjisiyle alakalı, momentum da enerjiyle alakalıdır.) Çıkan 2 foton, tek bir pure entangled state'tedir:
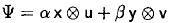
Laser beam (pump beam) nonlinear crystal'den geçerken, dolanık foton çiftleri oluşuyor.
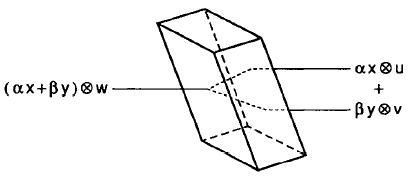
Özellikler
- Gelen ışının polarization state'i elliptic (bileşenleri mutually orthogonal), çıkan fotonların polarization'ı linear. (alfa x+beta y) polarization bilgisi, x ve y bileşenlerine ayrılarak farklı fotonlara aktarıldı. x ve y birbirine orthogonal. 2 photons have perpendicular polarizations. This is Type-II down conversion. Type-II: no polarization correlation.
- Gelen ışın, w lokasyonunda veya momentumunda, çıkan ışının biri u lokasyonunda/momentumunda biri v lokasyonunda/momentumunda. Sonuçta momentum korunuyor.
- Gelen ışın: mixed değil pure çünkü polarization vektör formunda yazılabilir ve tek olasılık var: 1 olasılıkla gelen ışın alfa x+beta y olabilir.
- alfa x tensor u ve beta y tensör v belirli olasılıklarla oluşmuyor, 2 ayrı durum birden oluşuyor, bundan dolayı çıkan durum mixed değil pure state'tir. Yani hep aynı girdi hep aynı çıktıyı alırsın. Bu yöntem, olasılıksal bir yöntem değil.
- w, u ve v'nin tensor çarpımı olarak yazılmış. u ve v farklı Hilbert space'lere ait olduğu için tensör çarpımı kullanılmış. w momentum olsaydı w=u+v yazılırdı.
- Incident beam is an uncorrelated direct product. Çıkan durum: One photon is correlated to the other one.
- Type I gerçekleşseydi, özdeş parçacıklar kullanılarak üretilen EPR state şu olurdu:
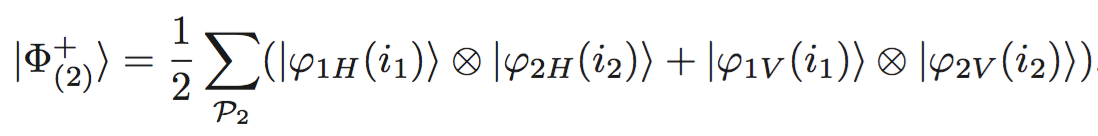
State'ten görüldüğü üzere ya iki parçacık da horizontal ya iki parçacık da vertical polarization'a sahip olurdu.
- Spatial degrees of freedom (locations of path) olarak fotonların momentum yönlerini alabiliriz. (Spatial degrees of freedom are various directions of the momentum of the photons.) Polarizasyon ve uzaysal mod, 2 farklı serbestlik derecesi. Bir de uzaysal mod da kendi içinde farklı serbestlik derecelerine ayrılabilir, farklı modlar farklı serbestlik dereceleri olabilir bence.
- Gelen fotonun polarizasyonu eliptik (horizontal ve vertical bileşenleri var). Çıkan bir foton ya vertical ya horizontal polarizasyona sahip. Çıkan bir fotonun polarizasyonu, gelen fotonun polarizasyon serbestlik derecesinin modlarının (horizontal ve vertical) lineer kombinasyonu şeklinde yazılmıyor. Bu yüzden kristalimiz nonlinear'dır.
Fock States
Fock state'ler adedinin belli olduğu ya da olmadığı identical particle'ların ifadesi için geliştirilmiştir. n, özdeş parçacık sayısı olmak üzere farklı n'ler üstünden convex sum vardır. Convex sum'ların arasındaki state'ler parçacık sayısı ile etiketlenir. Parçacıklar özdeş olduklarından dolayı symmetrizing ya da antisymmetrizing işlemi gereklidir. Örneğin n=3 parçacık için ya da n=2 parçacık için oluşturulan symmetrized state entangled görünümündedir. Çünkü topluca bir dalga fonksiyonları vardır ve bu dalga fonksiyonu dolanık formdadır. Kendi doğalarında dolanıklık var görünüyor çünkü dalga fonksiyonu 1'den fazla parçacık içindir ve separable değildir.
Operatör tabanlı bir metottur (Operator-based method).
n'ler occupation number'dır. Yaratma, yok etme operatörleriyle ifade edilir durumlar.
Yaratma yok etme op.larıyla yapıldığı için second quantization'a girer.
Geleneksel olarak kullandığımız state-based method ise first quantization'a girer.
1st quantization'da dalga fonksiyonları vardır. 2nd quantization'da parçacıklar vardır. Displacement field'lar vardır, bunlar parçacık gibi düşünülür. Koordinat alanı (ya da alan koordinatı) ya da momentum alanı (ya da alan momentumu) kavramları vardır. Alan koordinatı ve alan momentumu, yaratma yok etme operatörleri ve free particle (serbest parçacık) fonksiyonlarının karışımıyla yazılır.
Second quantization'a gereksinim şuradan doğmuştur: Schrödinger dalga denkleminden parçacığın sadece dalga özelliğini görüyor olmamız, parçacık özelliği ile çalışamamamızdır. Parçacık özelliğiyle çalışmak için böyle bir metot yaratmışız.
Soru: Genişliği 0'dan a'ya kadar olan bir potansiyel kuyusunda bulunan 2 adet spin-\(\frac{1}{2}\) parçacığının (bunlar elektron olsun) taban durumu ve uyarılmış durum dalga fonksiyonları ve enerjileri nedir?
Yanıt: Harmonik osilatörün enerji seviyeleri n=0'dan başlar ancak burada n=1'den başlayacak.
Potansiyel kuyusundaki bir elektronun konumuna ait dalga fonksiyonu \(\psi=\sqrt{\frac{2}{a}}\sin{\frac{n \pi x}{a}}\)'dır. Dolayısıyla 2 elektron taban durumundayken konuma ait dalga fonksiyonları \(\psi_{taban}=\frac{2}{a}\sin{\frac{n_{1} \pi x_{1}}{a}}\sin{\frac{n_{2} \pi x_{2}}{a}}\) olup \(n_{1}\) 1.elektronun bulunduğu enerji seviyesi, \(n_{2}\) 2.elektronun enerji seviyesidir. İki elektron taban durumunda iken \(n_{1}=1\), \(n_{2}=1\)'dir. Toplam dalga fonksiyonunu konum ve spinör şeklinde yazalım. Elektronlar Fermi-Dirac istatistiğine tabi olduklarından toplam dalga fonksiyonları antisimetrik olmalıdır. Konuma ait dalga fonksiyonu, \(\psi_{taban}=\frac{2}{a}\sin{\frac{\pi x_{1}}{a}}\sin{\frac{\pi x_{2}}{a}}\), simetrik olduğundan spinörleri (spin vektörleri) antisimetrik yani singlet durumunda olmalıdır.
2 parçacığın açısal momentumlarının toplanması problemine bakalım. Burada parçacıklar özdeş olabilir, olmayabilir. Aşağıdakiler özdeş olup olmama konusundan bağımsızdır. Spin açısal momentuma bakalım. 2 parçacığın spin uzayı 2 farklı baz seti ile ifade edilebilir. Yani aynı uzayı geren 2 baz seti vardır. Birisi toplam açısal momentum değerlerinin oluşturduğu baz seti, diğeri iki elektronun bireysel ele alındığı baz seti.
1. baz setinin elemanları {s, m} yani {toplam spin değeri, spinlerin z-bileşenlerinin toplamı} cinsinden yazılır. İki s=\(\frac{1}{2}\) parçacığının alabileceği s değerleri, \(s_{1}\) ve \(s_{2}\)'nin toplamlarından mutlak değerce farklarına kadar olan tamsayılardır. Yani s=1, 0 değerlerini alabilir. Bunlara ait \(m_{s}=1, 0, -1\) ve \(0\)'dır. \(\ket{s m}=\ket{11}, \ket{10}, \ket{1-1}, \ket{00}\).
2. baz setinin elemanları {\(m_{1}, m_{2}\)} yani {1.parçacığın spininin z-bileşeni, 2.parçacığın spinin z-bileşeni} cinsinden yazılır. Baz setinin elemanları: \(\\\ket{m_{1} m_{2}}=\ket{++}, \ket{+-}, \ket{-+}, \ket{--}. \\+=+\frac{1}{2}= spin up, -=-\frac{1}{2}= spin down\)
Aynı uzayı geren 2 farklı baz setini birbirine bağlayan elemanlar, Clebsch-Gordon katsayılarıdır. Aşağıda, bir baz setinin elemanları diğer baz setinin elemanları cinsinden yazılmıştır. Tüm katsayılar CG katsayılarıdır.
\(\ket{11}=\ket{++}\\ \ket{10}=\frac{1}{\sqrt{2}}(\ket{+-}+\ket{-+})\\ \ket{1-1}=\ket{--}\\ \ket{00}=\frac{1}{\sqrt{2}}(\ket{+-}-\ket{-+})\\ \)Burada \(\ket{00}\) singlet'tir, antisimetrik durumdur.
Yukarıda \(\ket{+-}\) ile \(\ket{-+}\)'nın toplanması veya çıkarılması parçacıkların özdeş olması sebebiyle değildir. Sadece \(\ket{10}\)'a karşılık getirmek için toplanmıştır. 2.baz seti tabanında düşünürsek \(\ket{+-}\) ve \(\ket{-+}\) farklı durumlardır, özdeş durumlar değildir. Yani bu toplam özdeş parçacıkların permutasyonundan kaynaklı değildir. Ancak simetri ve antisimetri içerdiği için özdeş parçacıklar çalışılırken bu yönleri hesaba katılır.
\(m=0\) olan 2 tane durum vardır. s değerlerine bakmadan bunları nasıl ayırt ederiz? 2 parçacığın yer değiştirmesi/değiş tokuşu altında dalga fonksiyonunun nasıl değiştiğine bakarız. Eğer 2 parçacık \(\ket{10}\) durumundaysa değiştokuş yapıldığında dalga fonksiyonları simetrik olacaktır, \(\ket{00}\) durumundaysa antisimetrik olacaktır.
2 parçacıklı sistemi 1. baz seti ile çalışalım. Toplama ait olan \(\ket{s m}\) değerleri arasındaki geçiş (yani baz setini geren bazlar arasındaki geçiş) raising, lowering (indirme, çıkartma/merdiven) operatörleri ile yapılır. 2.baz seti ile çalışırken indirme \(S_{1-}\) veya \(S_{2-}\)'dir. Daha açık ifadeyle de \(S_{1-}\otimes\mathbb{1}_{2}\) veya \(\mathbb{1}_{1}\otimes S_{2-}\)'dir. Yani en yüksek durumdan bir alt duruma geçerken iki parçacıktan birini değiştiriyoruz. İki baz setini birbirine bağlarken görülüyor ki \(S_{-}=S_{1-}+S_{2-}\) çıkıyor. Daha açık ifade \(S_{-}=S_{1-}\otimes \mathbb{I}_{2}+\mathbb{I}_{1}\otimes S_{2-}\)'dir.
\(S_{-}\ket{s,m}=\hbar\sqrt{(s+m)(s-m+1)}\ket{s,m-1}\)
\(S_{-} \ket{11}=\hbar\sqrt{2}\ket{10}= \\(S_{1-}\otimes \mathbb{I}_{2}+\mathbb{I}_{1}\otimes S_{2-}).\ket{++}=\hbar(\ket{-+}+\ket{+-}) \\ \Rightarrow \ket{10}=\frac{1}{\sqrt{2}}(\ket{+-}+\ket{-+})\)
\(\psi_{taban}=\frac{2}{a}\sin{\frac{\pi x_{1}}{a}}\sin{\frac{\pi x_{2}}{a}}\otimes\ket{00} \\ E_{n_{1},n_{2}}=\frac{(n_{1}^2+n_{2}^2)\pi^2\hbar^2}{2ma^2} \\E_{taban}=\frac{(1^2+1^2)\pi^2\hbar^2}{2ma^2} \)
\(\psi_{uyarılmış}=\frac{1}{\sqrt{2}}\frac{2}{a}(\sin{\frac{\pi x_{1}}{a}}\sin{\frac{2 \pi x_{2}}{a}}-\sin{\frac{2 \pi x_{1}}{a}}\sin{\frac{\pi x_{2}}{a}})\otimes(triplet'lerden biri) \\ (n_{1}=1, n_{2}=2 + n_{1}=2, n_{2}=1) \) veya \(\psi_{uyarılmış}=\frac{1}{\sqrt{2}}\frac{2}{a}(\sin{\frac{\pi x_{1}}{a}}\sin{\frac{2 \pi x_{2}}{a}}+\sin{\frac{2 \pi x_{1}}{a}}\sin{\frac{\pi x_{2}}{a}})\otimes(singlet) \\ E_{uyarılmış}=\frac{(1^2+2^2)\pi^2 \hbar^2}{2ma^2}\)
Uyarılmış dalga fonksiyonunda konum fonksiyonu antisimetrikse spinör simetrik; simetrikse antisimetrik. Bir de yukarıda spatial wavefunction'da toplama veya çıkarma yapıyoruz ya onun sebebi parçacıkların özdeş olması, antisimetrik overall dalga fonksiyonu özelliği gösterecek olması. Öyle olmasaydı tek tek parçacıkların spatial dalga fonksiyonlarını ve spinörlerini dış çarpımla çarpardık.
Pauli Dışarlama İlkesi
Overall wavefunc = spatial wavef * spinor
n: principle quantum number, enerji ile ilgili
r1, r2: konum bilgisi
Two-particle wave functions for indistinguishable fermions:
| Overall | spatial | spin |
|---|
| |
antisimetrik \(\Psi\): (-) |
simetrik spin: (+) |
\(\Psi= A[\psi(n_{1},r_{1})\psi(n_{2},r_{2})-\psi(n_{1},r_{2})\psi(n_{2},r_{1})]\)
\(r_{1}\) konumundaki parçacık 1.enerji durumunda, \(r_{2}\) konumundaki parçacık 2.enerji durumunda ya da \(r_{2}\) konumundaki parçacık 1.enerji durumunda, \(r_{1}\) konumundaki parçacık 2.enerji durumunda. Ya da ifadesi (- işareti) ayırt edemediğimizden dolayı geliyor. |
spin triplet durumlarından biri:
X(1,1)=X+X+
X(1,0)=1/sqrt(2) (X+X- + X-X+)
X(1,-1)=X-X- |
|
simetrik \(\Psi\): (+) |
antisimetrik spin: (-) |
\(\Psi\)= A(\(\psi\)(n1,r1) \(\psi\)(n2,r2) + \(\psi\)(n1,r2) \(\psi\)(n2,r1) )
1.parçacık r1 konumunda, 2.parçacık r2 konumunda ya da 1.parçacık r2 konumunda, 2.parçacık r1 konumunda. Ama 2 parçacık da aynı enerji düzeyinde. |
spin-singlet:
X(0,0)=1/sqrt(2) (X+X- - X-X+) |
Fermiyonlar aynı enerji seviyesinde bulunuyorsa konumları farklıdır. Çekirdeğin etrafında aynı enerji seviyesinden bulunup farklı konumlarda olabilirler. Simetrik dalga fonksiyonunu yazarken aynı enerji seviyesinde iseler aynı konumlardadır yanılgısına düşme.
Yukarıda spin triplet durumunda neden 1/sqrt(2)*(up up + up up) ve 1/sqrt(2)*(down down + down down) değil? Bunlar ayırt edilemez oldukları için exchange symmetry'yi dalga fonksiyonlarını yazarken yaptığımız gibi spinlerini yazarken de yapmalıyız?
Permutation Symmetry for Identical Particles
2 particles
Permutasyon operatörünü 2 bozona ait bir duruma vurarak yarattığın uzay, eş uzay oluyormuş.
If Hamiltonian is invariant under interchange of the two particles, it must be the case that P12H = HP12. H and P12 possess a complete set of common (ortak) eigenvectors. Because (P12)2=I, the only eigenvalues P12 are +1 and -1, and its eigenfunctions are either symmetric or antisymmetric.
3 particles
3 parçacığın 6 permutasyonu olur, dolayısıyla 6 permutasyon operatörü tanımlayabiliriz:
- identity operator I
- the pair interchange operators P12, P23, P31
- the cyclic permutations P123
- (P123)2 Bu nedir?

3 parçacığa ait permutasyon operatörleri 6D vektör uzayını gererler.
6 permutasyon operatörü mutually commutative değildir: P12P23=değil P23P12. Therefore complete set of common eigenvectors for these opearators does not exist. Dolayısıyla H'nin her özvektörü için simetrik veya antisimetrik olma söz konusu değil.
Demek ki P'ler komütate etmiyorsa H'nin her özvektörü simetrik ya da antisimetrik değilmiş!
Fakat bu 6 boyutlu vektör uzayını invariant büyüklükler verecek subspace'lere bölebiliriz. Bir altuzay içindeki bir vektör, permutasyon operatörüyle aynı altuzaydaki başka bir vektöre dönüştürülebilir.
4 tane altuzaya bölünmüş: Nasıl oldu bilmiyorum?

- Simetrik altuzay: pair interchange ve cyclic operatörlerle yapılmış. Pair interchange opları etkimesi sonucu oluşmuş bazların işareti (+) yapılmış. Uzay 6D.
- Antisimetrik altuzay: Simetrikle aynı elemanlar. Cyclic'lerin işareti (+), pair interchange'lerin işareti (-). Uzay 6D.
- Kısmi simetrik:
- Sanırım kısmi antisimetrik olacak:
Bunların uygulaması iyi olur! 3 parçacık permutasyon uygulaması bul.
Sanırım bir durum bir altuzay bazlarıyla yazılabiliyorsa durumun permutasyon operatörünün etkisiyle değişmesi durumunda bu altuzaya izdüşümü olan bir büyüklük invariant'tır.
H'nin eigenvector'leri bu altuzaylardan biri seçilerek o altuzayın bazlarıyla yazılabilir. Ama sanırım diagonal olmaz. Çünkü H tek bir bazda diagonaldir, dolayısıyla hepsinde olamaz(?).
Bir operatörün eigenket'leri vector space'tedir. Bu vector space, Hilbert space'tir. Sanal sayılar kompleks düzlemdedir. Bir dalga fonksiyonunu eigenket'lerle yazalım. Daha sonra bu eigenket'lerin önüne sanal genlikli faz gelsin. Bu arada vector space'imiz bir skaler ile çarılabildiği ve skaler dediğimiz şey kompleks sayı olduğu için bu vektör uzayı, kompleks vektör uzayıdır. Adı budur. Ancak bazları kompleks sayıyla çarparsan nasıl bir geometrik şekle gidersin?
Inner product vs dot product
Inner product is the general one. Dot product is a special case. In inner product, vectors are the elements of a complex vector space. In dot product, vectors are the elements of Euclidean space. Inner product of two vectors is a complex number (as in general). Dot product of two vectors are a real number.
Infinite Square Well / Potential Well
Infinite square well has a certain length \(a\), the well is defined in-between \(x=[0,a]\). The walls of the well are represented by a potential energy. The potential energy, shortly the potential, \(V(x)\) is time-independent. There is an electron inside the well.
By solving Schrödinger wave equation
\(i\hbar \frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}+V(x)\psi(x,t)\)
for the length of the well and for \(V(x)\), we can obtain \(\psi(x,t)\) of the electron. The method of separation of variables: \(\psi(x,t)=\psi(x)T(t)\). We focus to find \(\phi(x)\).
Time independent Schrödinger equation (TISE): \(\phi''+(\frac{2mE}{\hbar^2})\phi=0\). NOTE: the coeff. of \(\phi\) is constant.
The solution of the differential equation (DE) is, in general, a linear combination of even and odd functions: \(\phi(x)=A\sin{(kx)}+B\cos{(kx)}\)
By applying boundary conditions (BC), we find a more specific solution (\(\phi_n(x)=A\sin{(\frac{n\pi x}{a})}\)).
By using normalization condition, we find the coefficient (\(A=\sqrt{\frac{2}{a}}\)).
Symmetric Infinite Square Well
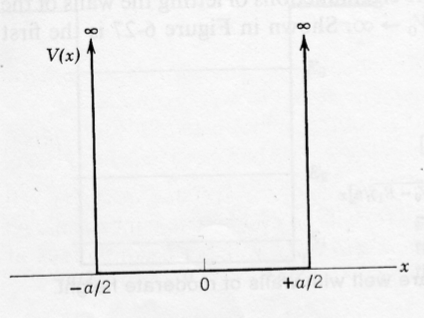
By shifting the well from \(x=[0,a]\) to \(x=[-\frac{a}{2},\frac{a}{2}]\) the solution becomes either
\(\phi_n(x)=\sqrt{\frac{2}{a}}\sin{(\frac{n\pi x}{a})}\) with \(n=2,4,6...\)
or
\(\phi_n(x)=\sqrt{\frac{2}{a}}\cos{(\frac{n\pi x}{a})}\) with \(n=1,3,5...\).
Namely, we obtain alternating even and odd solutions.
Harmonic Oscillator / Harmonic Potential Well
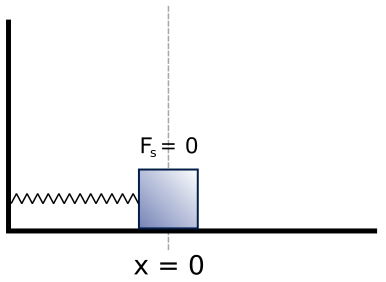
There is a mass connected to a spring. All the movement is in x direction (parallel to the ground). In equilibrium, \(m\) is at \(x=0\).
Total energy of the mass: Kinetic energy and potential energy caused by the spring (\(V(x)=\frac{1}{2}kx^2=\frac{1}{2}m\omega_c^2 x^2\)).
Solve TISE for \(V(x)\).
\(-\frac{d^2\phi}{dx^2}+\Big(\frac{2mE}{\hbar^2}-\frac{m^2\omega_c^2}{\hbar^2}x^2\Big)\phi(x)=0\)
The coef. of \(\phi\) is not constant. We cannot solve the DE as we did in previous section. We should use the method of power series. First, we need to make the DE dimensionless/unitless: \(q\equiv\beta x\)
\([x]=m\) \([\beta]=m^{-1}\)
\(\frac{d^2\phi}{dq^2}+\Big(\frac{2mE}{\hbar^2\beta^2}-\frac{m^2\omega_c^2}{\hbar^2\beta^4}q^2\Big)\phi(q)=0\)
- We equalize the coef. of \(q^2\) to 1. \(q^2\)'nin katsayısını 1'e eşitliyoruz. Because we want a \(\beta\) that makes the coef. of \(q^2\) is 1. \(q^2\)'nin katsayısını 1 yapacak bir \(\beta\) sayısı istiyoruz.
- For simplicity, we make \(\epsilon=\frac{2mE}{\hbar^2\beta^2}\). Sadelik için o ifadeye \(\epsilon\) dedik. \(\epsilon\) is dimensionless and it refers to energy.
\(\frac{d^2\phi}{dq^2}+\Big(\epsilon-q^2\Big)\phi(q)=0\)
BC makes \(\phi\) to take its form. So the solution of this equation becomes \(\phi(q)\approx h(q)e^{-\frac{q^2}{2}}\).
When you plug \(\phi\) into the previous equation, you obtain Hermite differential equations. Its solutions are Hermite polynomials \(H_n(q)\).
So the solution of that equation becomes \(\phi_n(x)=C_n H_n(\beta x) e^{-\frac{\beta^2x^2}{2}}\).
- \(C_n\): normalization constant
- \(H_n(\beta x)\): Hermite polynomials
- \(e^{-\frac{\beta^2x^2}{2}}\): Gaussian function.
Optical Cavity
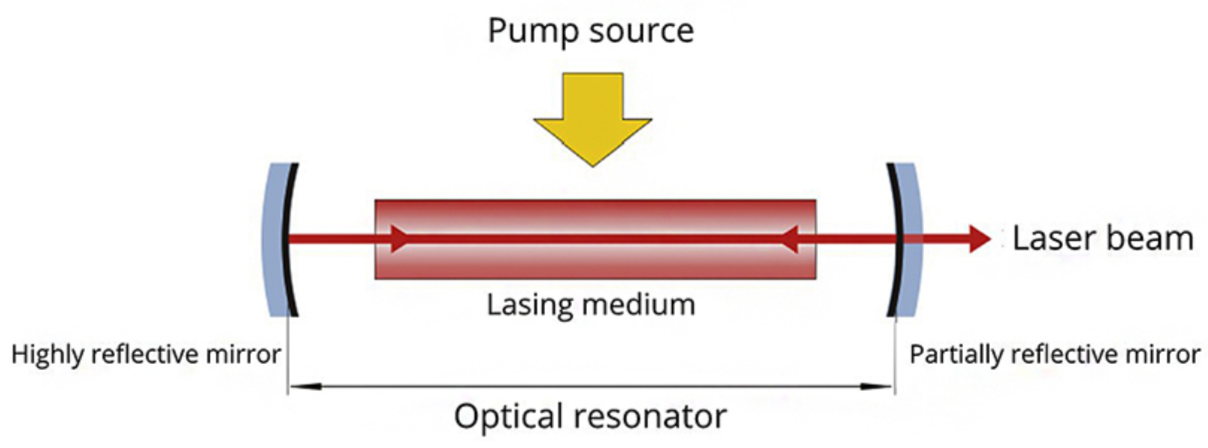
A photon between 2 reflective mirrors has standing-wave modes of electromagnetic field.
Cavity having spherical mirrors outputs Gaussian function (Gaussian beam).
I suppose a deflection from perfect spherical mirrors or depending on the length between the mirrors cause to deviate from (depart from) pure Gaussian function. And we start to obtain higher-order modes. The beam will be Hermite polynomials. The beam will be Hermite-Gaussian beam.
In symmetric potentials, generally, in quantum mechanics the wavefunction of the field/particle (in classical electromagnetism the solution of the beam (namely TEMmn modes)) constitute from Hermite polynomials and Gaussian function. When we have zero-order Hermite polynomial (\(H_0(q)=1\)), we should obtain pure Gaussian function. In case of higher-order modes, we start to deviate from pure Gaussian function and start to obtain Hermite polynomials.
Harmonic oscillator is symmetric about x=0 above. Symmetric potential well is symmetric about x=0 above. Optical cavity represents symmetric potential energy with 2 mirrors, so we work with even-odd functions (Hermite polynomials).