Melis Pahalı

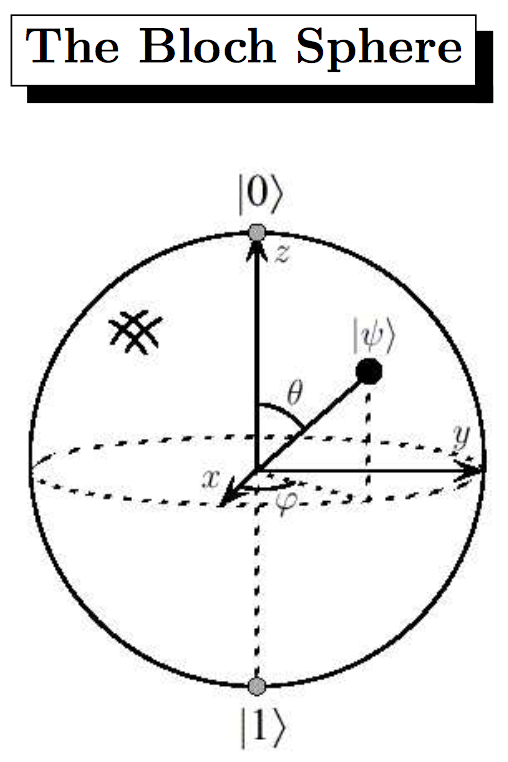
Bloch Sphere

2 seviyeli kuantum mekaniksel bir sistem, \(\ket{\psi}=z_0\ket{0}+z_1\ket{1}\) şeklinde yazılır. \(z_0, z_1 \in \mathbb{C}\)

\(z_0\) ve \(z_1\) kompleks sayıları, birer boyutlu kompleks sayılardır. Her kompleks sayı, 2 reel sayı içerir.

Bir sistem, 2-dimensional complex vector space'te gösterilir. 2 boyutu, \(z_0, z_1\) veya \(\ket{0}=\begin{pmatrix}1\\0\end{pmatrix}, \ket{1}=\begin{pmatrix}0\\1\end{pmatrix}\) oluşturur. Kompleks oluşu, katsayıların türü belirler.

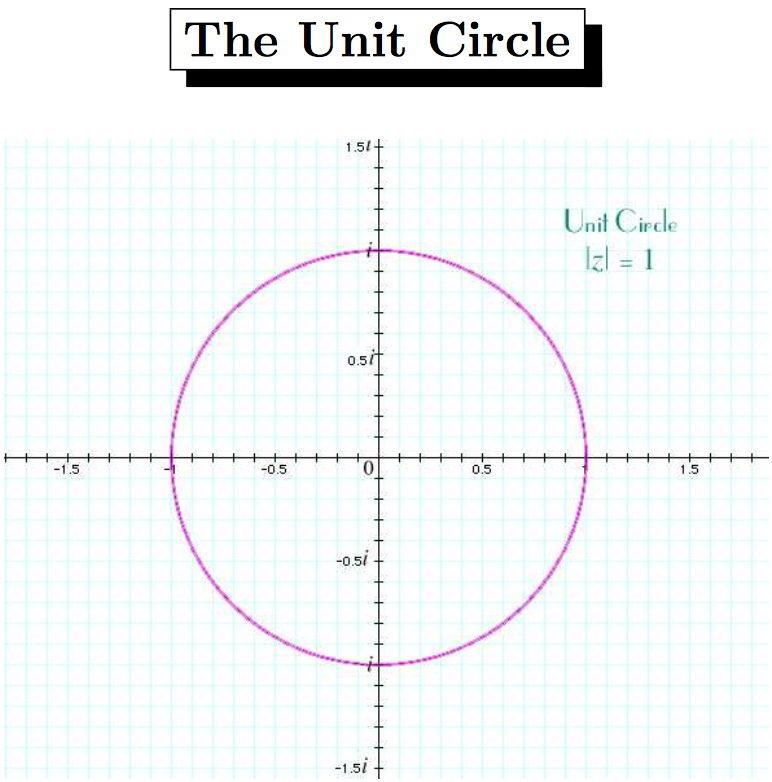
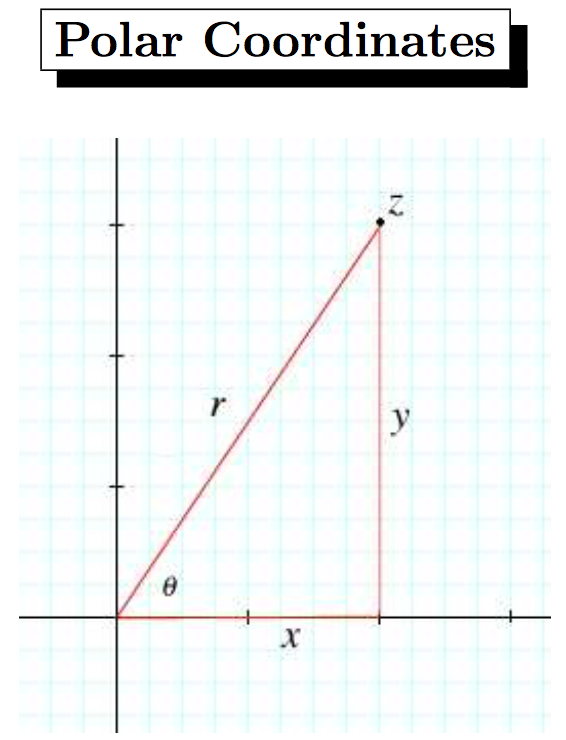
2 boyutlu complex plane'deki kompleks bir sayı iki şekilde gösterilebilir: \(z=x+iy, z=r e^{i \theta}\)

\(\ket{\psi}=r_0 e^{i \theta_0 }\ket{0}+r_1 e^{i \theta_1} \ket{1} \\e^{i \theta_0} \ket{\psi}=r_0 \ket{0}+r_1 e^{i(\theta_1 - \theta_0)} \ket{1} \\\ket{\psi}=r_0 \ket{0}+r_1 e^{i \theta} \ket{1}\)

Global phase'in fiziksel önemi yoktur, \(\ket{\psi}\) önündeki kompleks faz yazılmayabilir. Veya bir tane fazdan kaynaklanan bir fazlalığım vardı (\(\ket{0}\)'ın önünde), onu sildim. Elimde 3 reel sayı kaldı. \(r_0, r_1, \theta\).

\(\ket{\psi}=r_0 \ket{0}+(x+iy)\ket{1}\)

Normalization: \(\bra{\psi}.\ket{\psi}=1 \\r^*_0 r_0 +(x+iy)^*(x+iy)=1 \\\lvert r_0 \rvert^2+\lvert x+iy \rvert^2=1 \\r_0^2+(x-iy)(x+iy)=1\\ r_0^2+x^2+i(xy-yx)+y^2=1 \\r_0^2+x^2+y^2=1\)

This is equation of a unit sphere in real 3D space with cartesian coordinates \((x, y, r_0\)).

Cartesian coordinates are related to polar coordinates as: \(x=r \sin(\theta)cos(\phi)\\y=r \sin(\theta)\sin(\phi)\\z=r \cos(\theta)\)

Rename \(r_0\) to \(z\). For \(\ket{\psi}\) \(r=1\).

\(\ket{\psi}=r_0\ket{0}+(x+iy)\ket{1} \\=\cos(\theta)\ket{0}+(\sin(\theta)\cos(\phi)+i\sin(\theta)\sin(\phi))\ket{1} \\=\cos(\theta)\ket{0}+\sin(\theta)(\cos(\phi)+i\sin(\phi))\ket{1} \\=\cos(\theta)\ket{0}+\sin(\theta)e^{i \phi}\ket{1}\)

Birim küre üzerindeki noktaları tanımlamak için 2 parametre var: \(\theta,\phi\). Çalışma alanın kompleks düzlem yerine küresel koordinatlar oldu.

Bir kürede bir nokta \((r,\theta,\phi)\) ile belirlenir. Bu noktanın opoziti (opposite point) \((r,\pi - \theta,\phi + \pi)\) noktasıdır.

\(\ket{\psi}=\cos(\theta)\ket{0}+e^{i \phi} \sin(\theta)\ket{1} \\ \ket{\psi}_{opposite}=\cos(\pi - \theta) \ket{0}+e^{i(\pi + \phi)} \sin(\pi - \theta)\ket{1} \\=(\cos(\theta)\cos(\pi)-\sin(\pi)\sin(\theta))\ket{0}+e^{i \phi} e^{i \pi}(\sin(\pi)\cos(\theta)-\cos(\pi)\sin(\theta))\ket{1} \\=-\cos(\theta)\ket{0}-e^{i \phi} \sin(\theta)\ket{1} \\=-\ket{\psi}\)

Opozitine bakarken küreyi upper hemisphere, lower hemisphere diye ayırmış. Sistem için üst yarıküre unique kuantum-klasik eşleşmesi için yeterli. Çünkü bir nokta ile opoziti, aynı klasik bilgiye işaret ediyor.

Katsayılar uzayını küresel tutup (bildiğimiz gibi tutup) dalga fonksiyonunu revize ediyoruz:

\(\ket{\psi}=\cos(\frac{\theta}{2})\ket{0}+e^{i \phi} \sin(\frac{\theta}{2})\ket{1}\)

Katsayılar uzayı \(\theta\) için \(0\)'dan \(\pi\)'ye, baz uzayı \(\theta\) için \(0\)'dan \(\frac{\pi}{2}\)'ye kadar.

Dalga fonksiyonu, yarıkürede tanımlı. Katsayılar uzayında \(\ket{0}, \theta=0\) noktasında, \(\ket{1}, \theta=\pi\) noktasında. Kutup noktalarında \(\phi\)'nin önemi yok.

Bloch küresi \(x=sin\theta cos\phi \\ y=sin\theta sin\phi \\ z=cos\phi\) katsayılarının küresidir, \(\ket{0}\) ve \(\ket{1}\)'in değil.

Katsayılar uzayında dönme

x ekseni etrafında \(\pi\) kadar dönme (\(R_x(\pi)\)):

\(x \rightarrow x\\ y\rightarrow -y \\ z\rightarrow -z\)

x'in x'e, y'nin -y'ye, z'nin -z'ye gitmesi için \(\theta\) yerine \(\pi -\theta\), \(\phi\) yerine \(-\phi\) koymalıyız.

y ekseni etrafında \(\pi\) kadar dönme (\(R_y(\pi)\)):

\(x \rightarrow -x\\ y\rightarrow y \\ z\rightarrow -z\) için \(\theta \rightarrow \pi - \theta, \phi \rightarrow \pi - \phi\) koymalıyız.

z ekseni etrafında \(\pi\) kadar dönme (\(R_z(\pi)\)):

\(x \rightarrow -x\\ y\rightarrow -y \\ z\rightarrow z\) için \(\theta \rightarrow -\theta, \phi \rightarrow \phi\) koymalıyız.

Bloch sphere'ı döndürmek, katsayılar uzayını döndürmektir, \(\ket{0}\) ve \(\ket{1}\)'i döndürmek değil.

Katsayılar uzayında \(\pi\) kadar döndürmenin dalga fonksiyonunu ne hale getirdiğini görmek için dalga fonksiyonu ifadesinde \(\theta\) ve \(\phi\) yerine yeni ifadelerini koyuyorsun.

x ekseni etrafında dönme:

\(\ket{\psi}=\cos(\frac{\pi - \theta}{2})\ket{0}+e^{-i \phi} \sin(\frac{\pi - \theta}{2}) =e^{-i \phi}(\sin(\frac{\theta}{2})e^{i \phi}\ket{0}+\cos(\frac{\theta}{2})\ket{1})\)

x ekseni etrafında \(\pi\) kadar dönme (\(R_x(\pi)\)) Pauli X matrisini \(\ket{\psi}\)'ye vurmaya denktir.
y ekseni etrafında \(\pi\) kadar dönme (\(R_y(\pi)\)) Pauli Y matrisini \(\ket{\psi}\)'ye vurmaya denktir.
z ekseni etrafında \(\pi\) kadar dönme (\(R_z(\pi)\)) Pauli Z matrisini \(\ket{\psi}\)'ye vurmaya denktir.

\(\pi\) kadar döndürmek değil, en genel ifadeyle katsayılar uzayının dönmesiyle bazlar üzerinde operasyonlar şu şekilde ilişkili: \(R_x(\theta)\equiv e^{-i \theta X/2} \\ R_y(\theta)\equiv e^{-i \theta Y/2} \\ R_z(\theta)\equiv e^{-i \theta Z/2}\)